ASA Electronics AirClassic E6-B User manual

2
E6-B Flight Computer Instructions
This instruction booklet can be used with the three
different E6-B models available from ASA. If you
have a different model than the one depicted, some
parts of your computer may appear slightly different
from the computers pictured in this booklet. How-
ever, the calculations are accomplished with the
same method and produce the same answers.
© 1992 – 2000 ASA
Aviation Supplies & Academics, Inc.
7005 132nd Place SE
Newcastle, WA 98059-3153
All rights reserved. Reproduction in whole or in part of this text is
strictly prohibited and unlawful without the written permission of
Aviation Supplies & Academics, Inc.
ISBN 1-56027-421-2
ASA-E6B

3
Contents
Page
Instructions for Using ASA Flight Computer...... 4
The Slide Rule Side .......................................... 5
Time, Speed, and Distance Problems .............. 8
Fuel Consumption Problems ........................... 11
Conversions .................................................... 13
Nautical to Statute Miles ............................ 13
U.S. Gallons to Imperial Gallons ................ 15
Quantity/Weight Conversions..................... 16
Using the Altitude and Speed
Correction Windows ........................................ 18
True Airspeed and Density Altitude ................ 18
Converting Mach Number to True Airspeed.... 20
True Altitude .................................................... 21
Feet Per Mile vs. Feet Per Minute................... 22
Off-Course Problems ...................................... 24
The Crosswind Table ...................................... 27
The Wind Side of the Slide ............................. 28
Determining Winds in Flight ............................ 32
Answers to Sample Problems ......................... 37

4
Instructions for Using ASA Flight Computer
Your ASA E6-B Flight Computer has two main
parts: a circular slide rule side for making quick
calculations, and a wind side for computing ground
speed and wind correction angle. The slide portion
of the circular slide rule side also includes quick-
reference material.
Figure 1

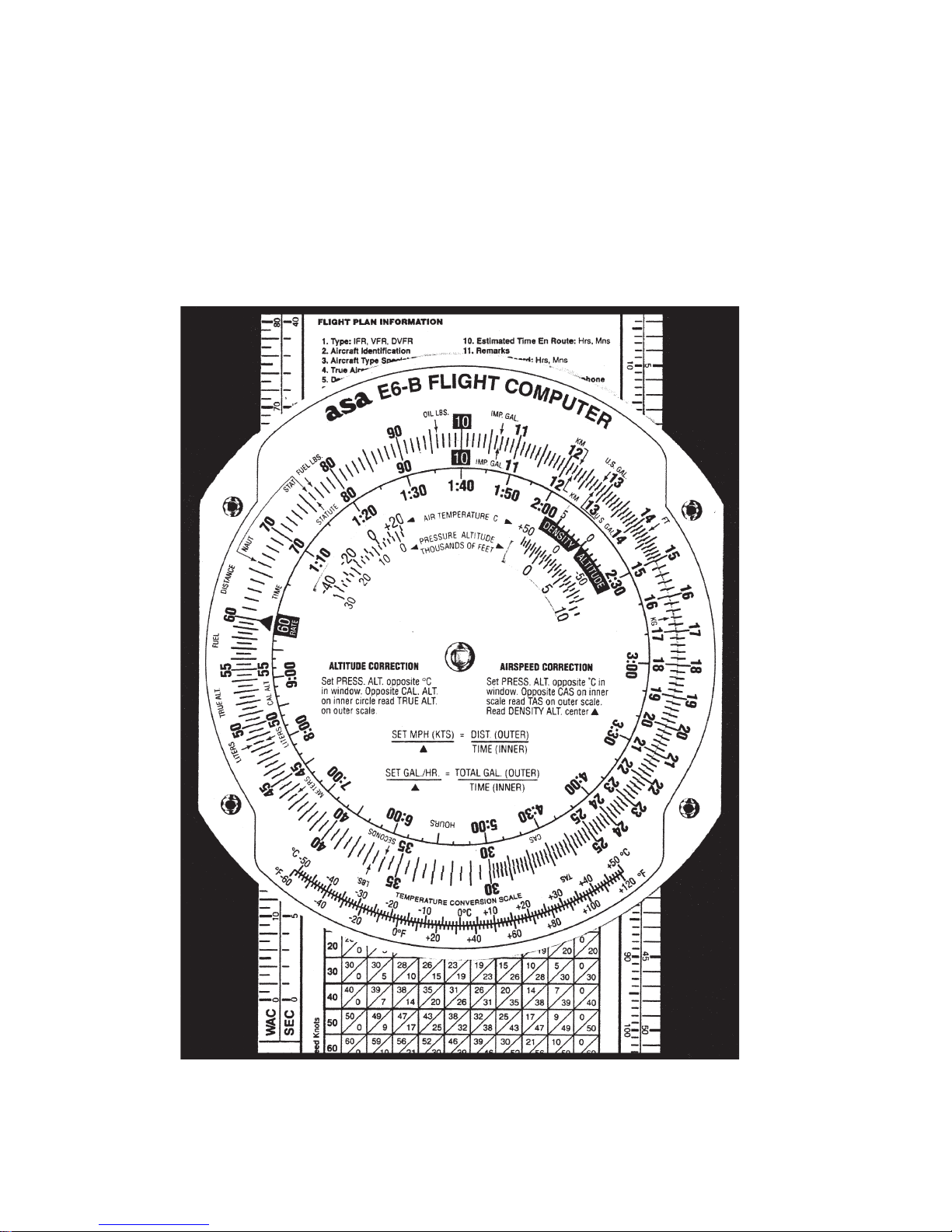
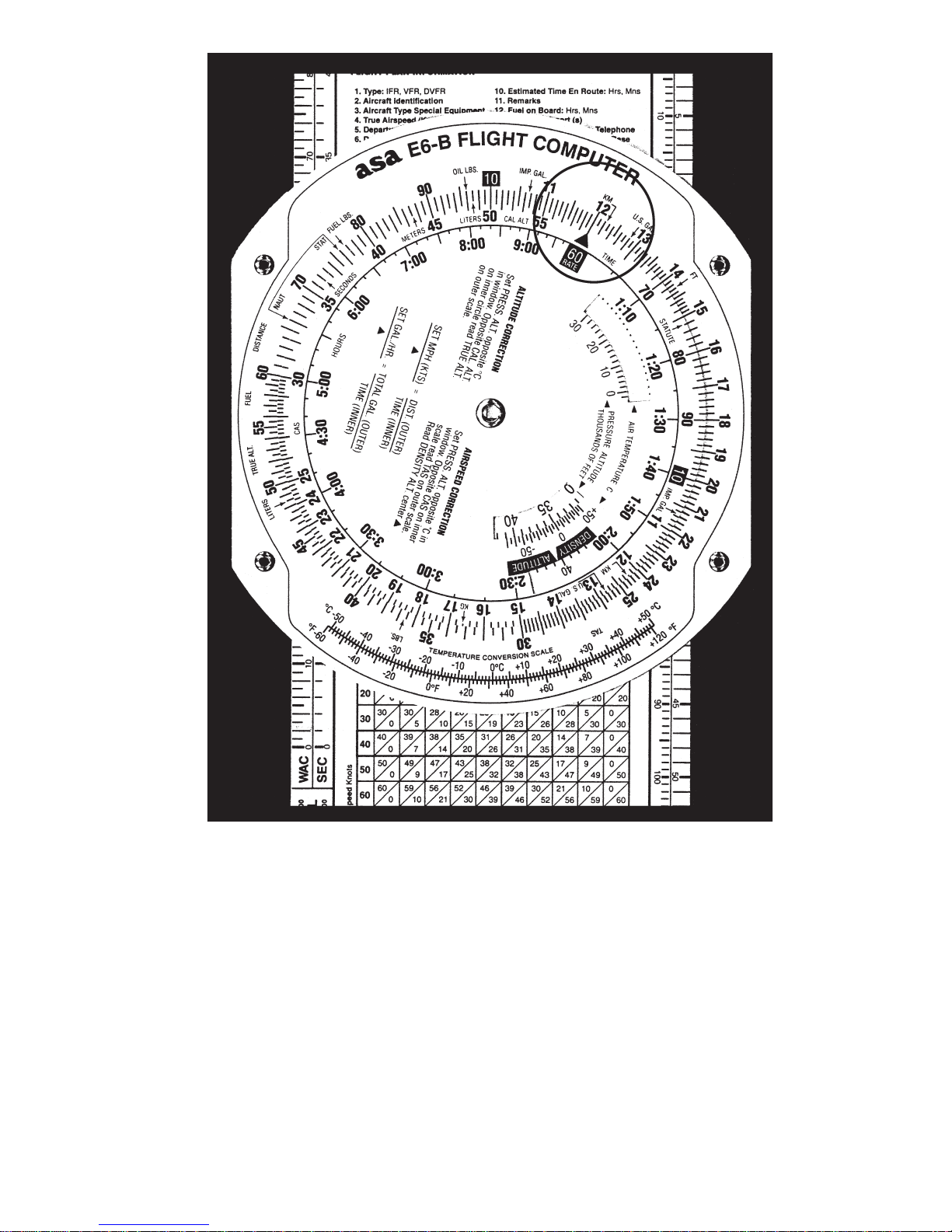
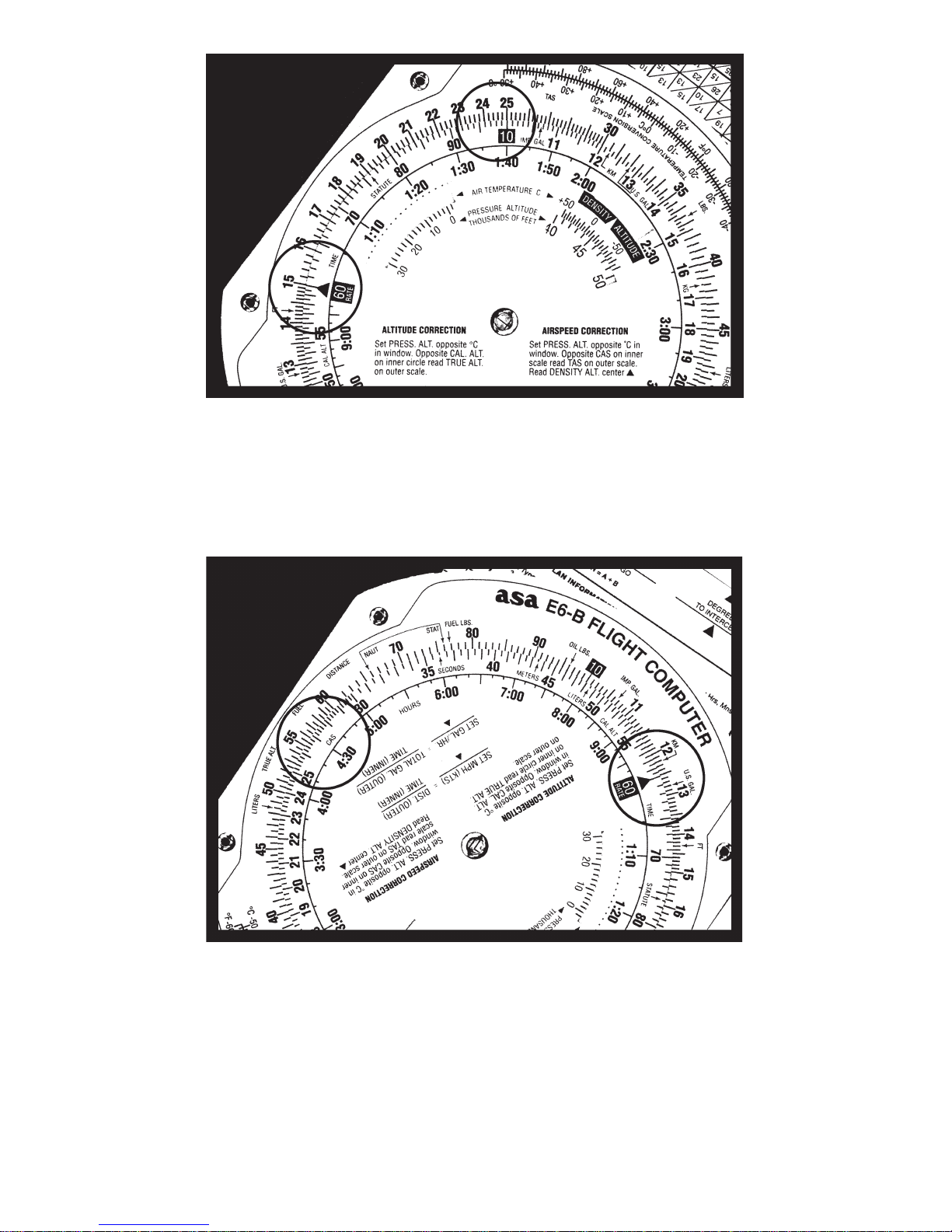
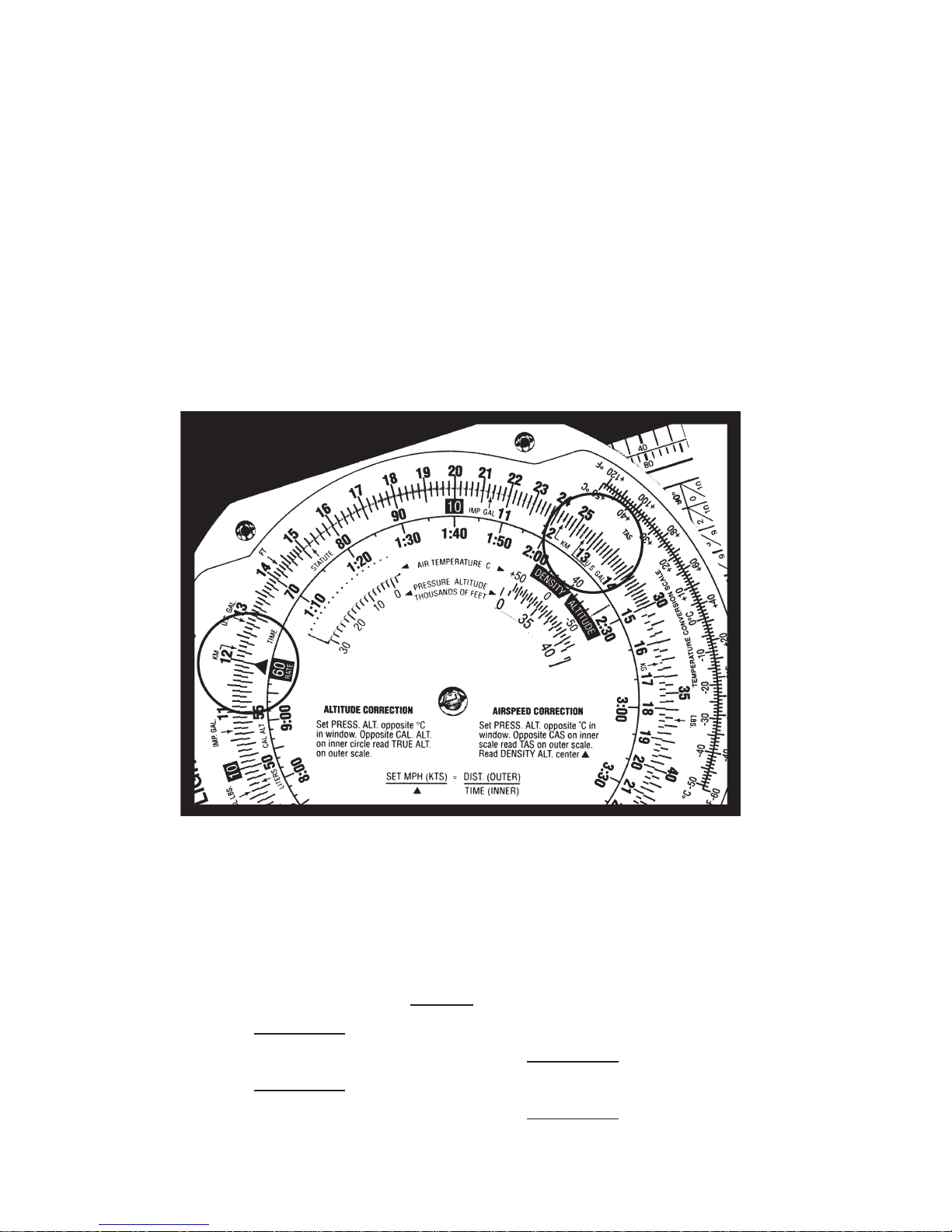
5
The Slide Rule Side
The term “circular slide rule” shouldn’t be intimidat-
ing. This side of your computer simply consists of a
rotating disk with numbers on the
middle scale,
which when set against similar numbers on the
fixed portion (
outer scale), allows you to solve
problems of time, speed, and distance, calculate
fuel consumption, and make conversions be-
tween measurements such as statute and nauti-
cal miles. The
inner scale on the rotating disk is
graduated in hours. The slide rule side also has
“windows” that you will use to solve airspeed and
altitude problems.
You can see that the number 60 on the rotating
disk is marked differently than the other numbers.
That is because most of your problems will be
concerned with time —“something” per hour, either
miles or gallons. Before you get to that, you should
learn how to read and interpret the numbers on both
portions of the slide rule side.
Rotate the disk until all of the numbers on the
middle scale match up with the numbers on the
outer scale —10 will be at the top. However, that
number “10” may be read as “.1,” “1,” “100,” or
“1,000”
depending upon the context of the problem .
For now, read it as 10. The next number to the right
is 11, so each life (or mark) of calibration between
the two numbers is equal to .1, and you would read
them as 10.1, 10.2, 10.3, etc. If you were solving a
problem involving 1,000 pounds of fuel, the number
10 would be read as 1,000, and each calibration
would be equal to 10 pounds, and the 11 would be
read as 1,100 pounds.
See Figure 1.

6
Now look at the number 15 on the disk. Between 15
and 16 each calibration mark is equal to .2 and
would be read as 15.2, 15.4, etc. If you were solving
a problem with an airspeed of 150 knots, the first
calibration past 15 (150 in this case) would be 152.
The spacing changes again at the number 30,
where each calibration becomes .5, and at 60,
where each calibration equals 1. Before you read a
value from the disks, be sure you understand what
each line of calibration is equal to.
You will use the slide rule side to establish
ratios. With the numbers matched, the ratio is 1 to
1. Now set the number 60 (the rate arrow) directly
opposite to (or, “lined-up” with) 12 on the outer disk
(
see Figure 2). Notice that all of the numbers on the
outer disk are exactly twice the value of the num-
bers on the inner disk: 90 is opposite of 180, 15 is
opposite of 30, 3.5 is opposite of 7.0. You will use
these ratios in solving time-speed-distance and fuel
consumption problems.
Look at the inside scale on the disk, where the
lines of calibration look like clock times: 9:00, 6:00,
etc.— these express hours. The inner scale is in
hours and the middle scale is in minutes. 1:10 is
directly below 70; one hour and ten minutes is the
same as seventy minutes. 5:00 is printed below 300
minutes, and five hours is the same as 300 minutes.
To convert minutes to seconds, place the rate arrow
opposite to the minutes on the outer scale and read
seconds opposite to the “seconds” arrow, just to the
right of 35 on the inner scale.

7
Figure 2. Line up the number 60 (the rate arrow) with
the number 12 on the outer disk (or, scale).

8
Time, Speed, and Distance Problems
The rate arrow on the disk is always set to indicate a
value per hour on the outer scale. There are three
basic time-speed-distance problems. In two of these
problems you know the rate, while in the third prob-
lem, the rate is part of the answer you are looking for.
To find the Time En Route, let’s assume you
know your airspeed is 150 knots (nautical miles per
hour).
1. Set the rate arrow to 150.
See Figure 3.
2. You have determined the distance to your
destination to be 245 nautical miles. Speed
and distance are always on the outer scale;
245 is halfway between 24 and 25.
3. Look directly opposite to that value on the
inner scale to find the Time En Route. It is
between 1:35 and 1:40. There are five cali-
bration marks on the middle scale between
1:35 and 1:40, and 245 NM on the outer scale
is closest to the third calibration, or one hour
and 38 minutes.
To find out how far you can go if your fuel
endurance is 4.5 hours and your ground speed is
known to be 125 knots:
1. Set the rate arrow at 125 on the outer scale.
See Figure 4.
2. Find 4:30 on the inner scale.
3. The value on the outer scale is slightly more
than 55. You know that 4 hours at 125 knots
should cover 500 miles, so the outer scale is
read as 500, not 50 or 5,000, which makes
each large calibration mark worth 10 nautical
miles. The answer is 564 nautical miles.

9
Figure 4
Figure 3

10
In the final and most common type of time-speed-
distance problem, the time and distance are known,
and you need to solve for unknown speed. The
rate arrow represents the answer. You will have
flown between two known ground reference points
26 NM apart and checked the time between them to
be: 13 (thirteen minutes, that is, not thirteen hours).
1. Set thirteen minutes on the middle scale op-
posite to 26 on the outer scale.
See Figure 5.
2. The rate arrow points to your ground speed,
120 knots.
Try these time-speed-distance problems:
(Answers are on Page 37)
SPEED TIME DISTANCE
1. 125 KTS 524 NM
2. 2:30 345
3. 110 KTS 1:40
4. 0:24 44
5. 95 1:24
Figure 5

11
Fuel Consumption Problems
Problems involving fuel consumption, fuel endur-
ance, and fuel capacity are solved using the same
numbers you used in the time-speed-distance prob-
lems. With the exception of time values, only the
names change.
Assume that your airplane’s Approved Flight
Manual indicates fuel consumption of 8.4 gallons
per hour at a given power setting and that the usable
fuel capacity is 64 gallons. How many hours endur-
ance do you have in the tanks?
1. Line up the rate arrow (“something per hour”)
with 8.4 on the outer scale.
See Figure 6.
2. Now find 64 on the outer scale.
3. Opposite of 64, read fuel endurance in hours:
7:37 on the inner scale. The outer scale,
which was used for speed and distance, is
now used to indicate gallons per hour and
fuel capacity.
Figure 6

12
When you paid for your fuel you noted on the
delivery ticket that it took 32 gallons to top the tanks.
You flew four hours and twenty minutes before
stopping for fuel. What was the average fuel con-
sumption? This time the rate arrow provides the
answer.
1. Set 4:20 on the inner scale (or 260 on the
middle scale) opposite of 32 on the outer
scale.
See Figure 7.
2. The rate arrow indicates the average fuel
burn rate: 7.4 gallons per hour.
Remember that fuel consumption is greater during
the climb to altitude, so this average value does not
accurately reflect fuel consumption in cruising flight.
Figure 7
Try these examples:
(Answers are on Page 37)
GALLONS PER HOUR TIME TOTAL USED
1. 7.8 3:20
2. 4:50 62
3. 8.5 38
4. 10 2:30
5. 12 22

13
Conversions
You can’t solve a problem unless the values agree.
You can’t mix statute and nautical miles, gallons
and liters, or Fahrenheit and Celsius. Your ASA
E6-B Flight Computer makes it possible for you to
convert between values with simple settings of the
middle scale.
Nautical to Statute Miles
Distances on sectional and world aeronautical charts
are in statute miles. Your airspeed indicator usually
reads in knots, or nautical miles per hour. It is easy
to convert between the two values by using special
markings on the slide rule side of your flight com-
puter. Look on the outside scale near 70 for mark-
ings labeled NAUT and STAT. Set the known value
under the appropriate arrow and read the converted
value under the other. For example, to convert 90
knots to statute miles per hour:
1. Set the arrow marked NAUT opposite of 90
on the middle scale.
2. Read 103.5 under the STAT arrow.
See
Figure 8.
Figure 8

14
You can convert either nautical or statute miles to
kilometers. Find the KM marking on the outer
scale. Set the known value beneath the NAUT or
STAT arrow as before, and read kilometers under
the KM marking. For example, to convert 115 stat-
ute miles to kilometers:
1. Set 115 opposite of the STAT arrow.
2. Read 185 under the KM marking.
See Figure 9.
Figure 9
Try these sample problems:
(Answers are on Page 37)
NAUT STAT KM
1. 20
2. 48
3. 110

15
U.S. Gallons to Imperial Gallons
Your Approved Flight Manual lists fuel capacity in
U.S. gallons, but in many countries fuel is delivered
in Imperial gallons. Arrows marked U.S. GAL and
IMP. GAL are provided on both middle and outer
scales to help you convert between these quanti-
ties. Your tanks are placarded to hold 64 U.S.
gallons. How many Imperial gallons will they hold?
1.
Line up the U.S. GAL arrow on the middle
scale opposite the IMP. GAL arrow on the
outer scale.
2. Find 64 on the middle scale.
3. Read 53.2 Imperial gallons on the outer scale
(
see Figure 10). Because Imperial gallons
are larger than U.S. gallons, the number of
U.S. gallons will always be larger.
Figure 10
You have purchased fuel in Canada and the deliv-
ery slip says 32 Imperial gallons. How many U.S.
gallons have you purchased? Line up the IMP. GAL
arrow with the U.S. GAL arrow. Find 32 on the

16
middle scale and read 38.5 U.S. gallons on the
outer scale.
Quantity/Weight Conversions
Aviation gasoline weighs 6 pounds per U.S. gallon.
For weight and balance calculations, aviation gaso-
line weight-per-gallon can be determined by lining
the U.S. GAL arrow on the middle scale with the
FUEL LBS arrow on the outer scale. Fuel gallons
are read on the middle scale and fuel weight on the
outer scale. To find the weight of 32 U.S. gallons:
1. Align the arrows.
2. Read 192 pounds on the outer scale opposite of
32 gallons on the middle scale.
See Figure 11.
Figure 11
Similarly, oil weight may be determined by lining the
U.S. GAL arrow on the middle scale with the OIL
LBS arrow on the outer scale. Oil gallons are read
on the middle scale and oil weight is read on the
outer scale. To find the weight of 2 gallons (8 quarts)
of oil:

17
1. Align the arrows.
2. Read 15 pounds on the outer scale opposite of
2 gallons on the middle scale.
See Figure 12.
Imperial gallon weight of fuel and oil may also be
determined in the same manner by lining up the
IMP. GAL arrow on the middle scale with the FUEL
LBS or OIL LBS arrow on the outer scale.
You can convert liters to U.S. gallons, pounds
to kilograms, or feet to meters by aligning the
appropriate arrows on the middle and outer scales.
For example, to convert pounds to kilograms:
1. Find the arrows marked LBS. and KG, and
line them up.
2. Any value in pounds on the outer scale will be
opposite of its converted value in kilograms
on the middle scale: 2,000 lbs is 901 kg, and
160 kg is 351 lbs.
3. The same procedure is followed for the other
conversions.
Figure 12

18
Using the Altitude and Speed
Correction Windows
Altimeters and airspeed indicators are designed to
give correct indications under standard conditions
at sea level. The consistency of the earth’s atmo-
sphere does not change linearly as you gain alti-
tude; its density is affected by variations in tempera-
ture and pressure. The E6-B provides windows on
the slide rule side so you can allow for these
variations when converting calibrated airspeed to
true airspeed or indicated altitude to true altitude.
True Airspeed and Density Altitude
Note that the outer scale of your flight computer is
marked TAS (true airspeed) and the middle scale is
marked CAS (calibrated airspeed).
The Approved Flight Manual for your airplane
contains a conversion table that allows you to
convert indicated airspeed to CAS. The difference
is greatest at low speeds and becomes negligible at
cruise speeds. To determine true airspeed you
must first know the pressure altitude. Set your
altimeter to 29.92 and read the altitude indicated;
that is the pressure altitude. Note the outside air
temperature and convert it to Celsius using the
conversion scale at the bottom of the flight computer.
1. Set the pressure altitude in the window oppo-
site the outside air temperature in Celsius.
2. Without moving the computer’s scales, read
the true airspeed on the outer scale opposite
CAS on the middle scale.

19
3. Read the density altitude over the arrow in
the DENSITY ALTITUDE window.
See Fig-
ure 13.
Figure 13 shows a pressure altitude of 15,000 feet
set opposite an outside air temperature of -15°C. A
calibrated airspeed of 145 knots converts to a true
airspeed of 183 knots and a density altitude of
15,000 feet under these conditions.
Here are some sample problems:
(Answers are on Page 37)
PRESSURE DENSITY
ALTITUDE TEMP CAS TAS ALTITUDE
1. 14,000 5°C160
2. 20,000 -20°C200
3. 8,000 15°C150
Figure 13

20
Converting Mach Number to True Airspeed
To convert Mach Number to True Airspeed (or vice
versa), rotate the inner dial until you see the Mach
No. Index inside the airspeed correction window on
the inner dial. Line up the true or outside air tem-
perature (do not use Indicated Air Temperature)
opposite this Mach No. Index. Mach Number on the
inner scale reads opposite True Airspeed (in nautical
miles per hour) on the outer scale. In Figure 14, at an
outside air temperature of +15°C and Mach 1 (10 on
the inner scale), read 661 knots on the outer scale.
Figure 14