Intel 2920 Guide

THE 2920 ANALOG SIGNAL PROCESSOR
DESIGN HANDBOOK
AUGUST 1980

Intel Corporation makes no warranty for the use of its products and assumes no responsibility for any errors which
may appear in this document nor does it make a commitment
to update the information contained herein.
Intel software products are copyrighted by and shall remain the property of Intel Corporation. Use, duplication or
disclosure is subject
to restrictions stated in Intel's software license, or as defined in ASPR 7-104.9 (a) (9). Intel Cor-
poration assumes no responsibility for the use of any circuitry other than circuitry embodied in an Intel product. No
other circuit patent licenses are implied.
No part
of this document may be copied or reproduced in any form or by any means without the prior written consent
of Intel Corporation.
The following are trademarks
of Intel Corporation and may only be used to identify Intel products:
BXP Intelevision
CREDIT Intellec
i iSBC
ICE iSBX
ICS Library Manager
im MCS
Insite Megachassis
Intel Micromap
MULTIBUS·
MULTIMODULE
PROMPT
Promware
RMX
UPI
,",Scope
and the combinations of ICE, iCS, iSBC, MCS or RMX and a numerical suffix.
MDS is an ordering code only and is not used as a product name or trademark. MDS® is a registered trademark of
Mohawk Data Sciences Corporation.
"MULTIBUS is a patented Intel bus.
Additional copies
of this manual or other Intel literature may be obtained from:
Literature Department
Intel Corporation
3065 Bowers Avenue
Santa Clara, CA 95051
© INTELCORPORATION,1980 AFN-01300A-1

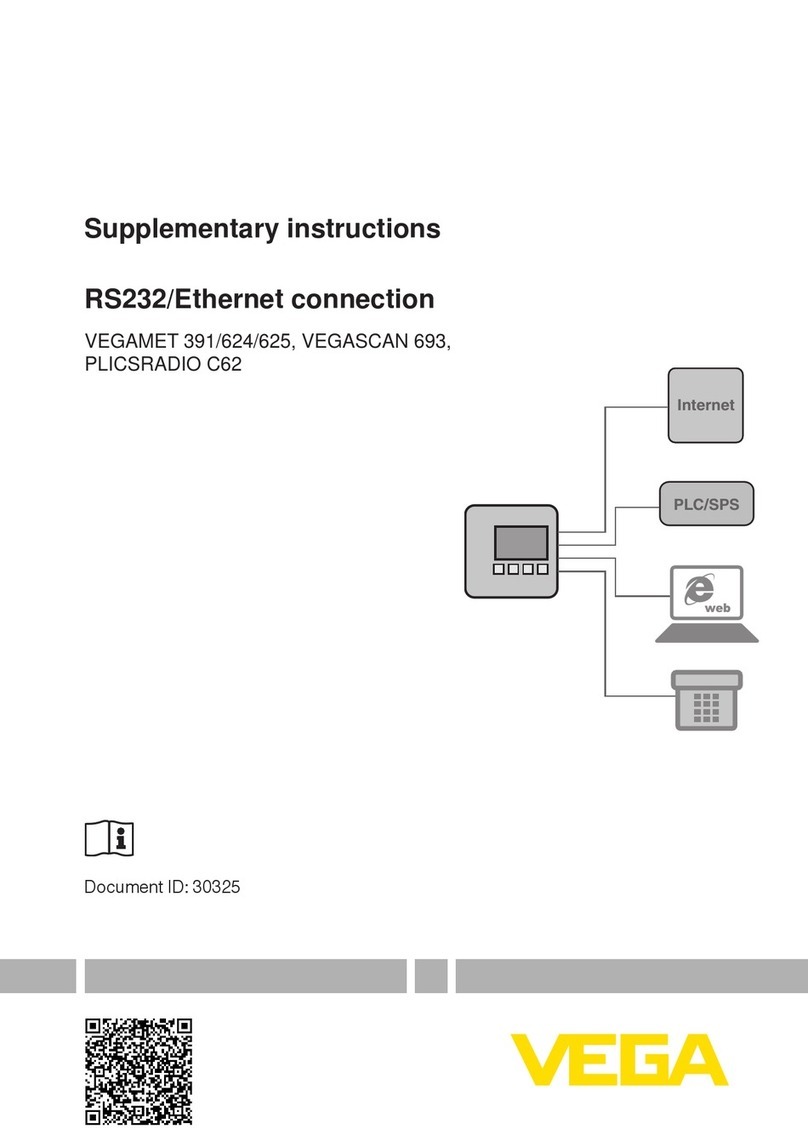
TABLE OF CONTENTS
1.0 INTRODUCTION AND TERMINOLOGY
1.1 The 2920 Signal Processor ............................................................. 1-1
1.2 Typical 2920 Design Sequence ......................................................... 1-2
1.3 Benefits of the 2920 Signal Processor Approach ......................................... 1-4
1.3.1 2920 Device Benefits ............................................................ 1-4
1.3.2 Deveiopment-Support-Tool Benefits ............................................. 1-4
2.0 SAMPLED DATA SYSTEMS
2.1 Elements ofa Digital Sampled Data System ............................................. 2-1
2.2 Effects of Sampling ................................................................... 2-2
2.2.1 Aliasing Noise .................................................................. 2-3
2.2.2 Signal Reconstruction Distortion ................................................. 2-4
2.2.3 Jitter Noise ..................................................................... 2-5
2.2.4 Quantization Noise .............................................................. 2-6
3.0 THE 2920 SIGNAL PROCESSOR
3.1 Device Operation ................. . . . . . .. . . . .. . . . . .. . . .. . . . . . . .. . . . .. . . . . . . . . . . . . . . . .. 3-1
3.1.1 Overview of the 2920 ............................................................. 3-1
3.1.2 Analog Operations .............................................................. 3-2
3.1.3 DigitalOperations ............................................................... 3-2
3.2 A Closer Look at the Functional Elements ............................................... 3-2
3.2.1 EPROM Section ................................................................. 3-2
3.2.2 Arithmetic Unitand Memory ..................................................... 3-3
3.2.3 The Analog Section ............................................................. 3-7
3.3 Basic 2920 Performance Parameters and Limits ........................................ 3-10
4.0 BUILDING BLOCK FUNCTIONS-FOUNDATION OF DESIGN
4.1 Arithmetic Building Blocks ............................................................. 4-1
4.1.1 Elementary Arithmetic ........................................................... 4-1
4.1.2 Multiplication by a Constant ...................................................... 4-1
4.1.3 Multiplication by aVariable ...................................................... 4-3
4.1.4 Division by aVariable ............................................................ 4-5
4.2 Realizing Relaxation Oscillators ........................................................ 4-6
4.2.1 Reset Technique for Relaxation Oscillator ........................................ 4-6
4.2.2 Overflow Technique for Relaxation Oscillator ..................................... 4-7
4.3 Voltage Controlled Oscillators (VCO's) ................................................. 4-7
4.4 Oscillators Based on Unstable Second-Order Section ................................... 4-8
4.5 Gain Controlled Oscillator ............................................................. 4-8
4.6 Realization of Non-Linear Functions .................................................... 4-9
4.6.1 Simulation of Rectifiers .......................................................... 4-9
4.6.2 Simulation of Limiters ........................................................... 4-9
5.0 SUMMARY OF FILTER CHARACTERISTICS
5.1 Characteristics of "Ideal" Filters ....................................................... 5-1
5.1.1 The Rectangular Filter ........................................................... 5-1
5.2 Minimum Phase Filters ................................................................ 5-2
5.2.1 Butterworth Filters .............................................................. 5-2
5.2.2 Chebyshev Filters ............................................................... 5-2
5.2.3 Elliptic Function Filters .......................................................... 5-2
5.2.4 Bessel and Gaussian Filters ..................................................... 5-3
5.2.5 Transitional GaussianlButterworth Filters ........................................ 5-3
5.2.6 Other Minimum Phase Filters .................................................... 5-3
5.2.7 Comparison of Minimum Phase Filters ...............................•............ 5-3

TABLE OF CONTENTS
5.3 Non-Minimum Phase and Allpass Networks ............................................. 5-4
5.4 Review of Analog FilterCharacteristics ................................................. 5-4
5.4.1 Effects of Pole/Zero Location on Filter Parameters ................................ 5-4
5.4.2 Transient Response and Selectivity ................... , .......................... 5-5
5.5 Digital Filters ......................................................................... 5-6
5.2.1 IIR Filters ....................................................................... 5-7
5.5.2 FIR Filters ...................................................................... 5-7
5.5.3 Canonical Forms of Digital Filters ................................................ 5-7
5.5.4 Matched ZTransform ............................................................ 5-9
5.5.5 Bi linearTransform ............................................................. 5-10
5.6 Implementing Filters with the 2920 ..................................................... 5-11
5.6.1 Simulating Single Real Poles .................................................... 5-12
5.6.2 Simulating Complex Conjugate Pole Pairs ....................................... 5-13
5.6.3 Realizing Zeros in Basic FilterSections .......................................... 5-14
5.6.4 Complex Conjugate Zero Pairs .................................................. 5-14
5.6.5 Some Practical Considerations .................................................. 5-15
5.6.6 Very Low Frequency Filters ..................................................... 5-16
5.6.7 Filters at a Multiple of the Sampling Rate ......................................... 5-17
5.6.8 Other Filter Structures .......................................................... 5-17
6.0 ADVANCED TECHNIQUES
6.1 Time VarIable Filters .................................................................. 6-1
6.2 Noise Generation with the 2920 ......................................................... 6-4
6.3 Digitallnput/Output .......................... ,......................................... 6-4
7.0 APPLICATION EXAMPLES
7.1 Sweeping Local Oscillator ............................................................. 7-1
7.2 Piecewise Linear Logarithmic Amplifier ................................................ 7-2
7.3 Digital Filter .......................................................................... 7-5
7.4 The 2920 as a Spectrum Analyzer ....................................................... 7-7
7.4.1 Description of Spectrum Analyzer ................................................ 7-7
7.4.2 Block Diagram Description ....................................................... 7-7
7.4.3 Sampled Data System Considerations ............................................ 7-9
7.4.4 Complete Spectrum Analyzer Assembly Listing .................................. 7-10
8.0 DESIGN CONSIDERATIONS
8.1 2920 Debugging Procedures ........................................................... 8-1
8.2 Description of Application Breadboard ................................................. 8-2
8.2.1 Layout Considerations .......................................................... 8-2
8.2.2 Parts List ....................................................................... 8-5
9.0 2920 SUPPORT TOOLS
9.1 The Assembler ....................................................................... 9-1
9.2 The Simulator ......................................................................... 9-1
9.2.1 Concept of Simulation, Testing and Debugging .................................... 9-1
9.2.2 Modes of Operation ............................................................. 9-2
9.2.3 A Generalized Simulation Session ................................................ 9-3
9.3 The 2920 Signal Processing Applications Software/Compiler ............................. 9-3
APPENDIX
REFERENCES
ii

Introduction
and Terminology 1

CHAPTER 1
INTRODUCTION AND TERMINOLOGY
1.0 INTRODUCTION AND
TERMINOLOGY
This handbook provides the background review and
design examples that will help the reader to understand
analog signal processing applications using INTEL's
digital signal processing system, the 2920. The 2920 uses
digital sampled
data techniques to implement con-
tinuous analog functions. In
another words, analog
signal processing can now be
performed with digital
signal processing techniques using the 2920.
Before looking at digital signal processing, it is useful to
clarify the distinctions between signal processing
and
digital processing. Signal processing deals with con-
tinuous analog waveforms, whereas digital processing
operates on data that are represented in a digital form.
Digital signill processing would then be the operation on
digital representation of continuous signals.
Digital signal processing, in the most general sense,
means creating, altering, or detecting continuous
signals, using digital rather than analog or electro-
mechanical implementations.
Furthermore, signal pro-
cessing can be distinguished from
data processing in
that the former implies that real-time processing is
needed. Data processing, however, implies the
manipulation of data (which mayor may not represent
an action occurring presently) in a batch or off-line
manner, where the need for the result is not a function
of real-time.
Most digital microprocessors are designed for data pro-
cessing, not for high-speed complex signal processing.
The industry-standard 8080/8085 microprocessor sys-
tem can operate as a signal processor at frequencies to
only a few hundred hertz, and will require mUltiple
chips with a separate analog/digital conversion system
and I/O circuitry.
By contrast, general signal processing frequencies are in
the kilohertz range (thousands of cycles per second).
Many signals, such as speech, heartbeat,
and seismic
waveforms are complex,
and in many cases, multiple
signals must be processed in parallel. Because
of dif-
ferent requirements for signal processing, a general pur-
pose microprocessor is not well suited for signal pro-
cessing applications. A different processor architecture
is required to implement signal processing algorithms.
1-1
1.1 The 2920 Signal Processor
The 2920 Signal Processor is a single chip microcom-
puter designed especially
to process real-time analog
signals.
The 2920 has on-board program memory,
scratchpad memory,
D/ A circuitry, A/D circuitry,
digital processor,
and I/O circuitry. It is more than a
single device, but is a complete digital sampled data
system. The architecture and instruction set was
developed to perform precise, high speed signal process-
ing. The processor executes its programs at typically
13,000 times a second when used with a
10 MHz clock
and full program memory. Each execution (1 pass of the
2920 program memory) can process up to four input
signals and up to eight analog output signals. The pro-
cessing speed allows signals with bandwidths to 5
kilohertz to be processed; shorter programs permit
higher
bandwidth. Its capabilities in signal processing
are diverse
and powerful, and include an extremely
broad range of applications.
Some of the signal processing functions the 2920 can
implement are shown in Table 1-1. It is important to
note that these are fundamental building block func-
tions which corresponds to functional blocks in an
application block diagram. These are some of the
building blocks
that can be linked together to implement
complex applications. Table 1-2 shows some of the
possible application areas for the 2920 Signal Processor.
The 2920 Signal Processor can implement any of the
listed functions under program control. Many functions
can be realized on the same chip. Interleaving multiple
inputs or outputs allows for several independent circuits
or a single highly complex one to be implemented. Even
higher complexity can be achieved by cascading 2920s.
If increased speeds are desirable, several 2920s can be
used in serial
or parallel to achieve this. In most cases,
complete signal processing applications are imple-
mented on a single device.
The 2920 Signal Processor is only part of the solution.
Since a large part of the cost in producing a product is
the development time needed to design, test, and inte-
grate the new circuit into the final
product, the 2920
support package has been developed. It provides the
software and
hardware necessary to take a design from
concept to implementation on the 2920 Signal Pro-
cessor. This system combines a standard INTEL Intellec
Series II microcomputer development system with the
signal processing
support package (SPS-20) to provide a
powerful set
of hardware and software support tools.
This
is described in Chapter 9.

INTRODUCTION AND TERMINOLOGY
Table 1-1. Signal Processing Functions
FILTERING
Complex poles and zeros
Arbitrary digital filter configurations
Multiple parallel or cascaded filter combinations
High accuracy and stability
WAVEFORM GENERATION
Arbitrary waveforms, e.g., sine, square, triangle, etc.
Broad frequency range with high resolution
9-bit amplitude accuracy
NONLINEAR FUNCTIONS
Full wave rectifiers
Limiters
Comparators
~ ANXN
Multiply/Divide
EX
PROCESSING
Controllable with external signals (analog or digital inputs)
Phase locked loops
Adaptive filters
MODULATION/DEMODULATION
Amplitude, frequency and phase modulation
Continuous or digital, e.g., FM and/or FSK
Analog or digital inputs and outputs
Pipeline processing using multiple 2920s
Table 1-2. Broadly Based 2920 Signal Processor Applications Base
TELECOMMUNICATIONS
DTMF /MF receivers
Modems
Tone/cadence generators
FSK/PSK mod/demod
Adaptive equalizers.
PROCESS CONTROL
Transducer linearization
Remote feedback control
Remote data link
Signal conditioning
SIGNAL PROCESSING
Waveform generators
Correia tors
Digital filters
Adaptive filters
Speech processing
Seismic processing
Sonar processing
Transducer linearization
1.2 Typical 2920 Design Sequence
Designing with the 2920 Signal Processor is best thought
of in terms of the building block functions it can imple-
ment
and the application models already available as
2920 routines (see Chapter 7). The designer should COn-
sider short 2920 assembly language routines as tools
which can be combined to achieve the desired system
function.
1-2
GUIDANCE AND CONTROL
Missile guidance
Torpedo guidance
Motor control
SPEECH PROCESSING
Vocoders
Speech analysis
Pitch extraction
Speech synthesis
Speech recognition
TEST AND INSTRUMENTATION
Phase locked loops
Frequency locked loops
Scanning spectrum analyzer
Digital filters
INDUSTRIAL AUTOMATION
Position and rate control
Communication links
Servo links
The first operation for the designer is to develop a
detailed system block diagram similar to one for a con-
tinuous analog design. Each block is then realized in
2920 code and arranged in a suitable sequence. The 2920
Signal Processing Applications Software/Compiler
(SPAS-20) can be used interactively to facilitate
developing the precise code to meet design constraints.
The code can then be assembled as individual functional
blocks or as an entire system. Once the functions or
system has been assembled, it can be debugged via use
of the simulator.

INTRODUCTION AND TERMINOLOGY
The AS2920 Assembler tests the logical sequence, syn-
tax,
and editing of the program, and issues error or
warning messages. When assembly is successful, the
code used to
program the EPROM is created. This code
is also used as the program input to the SM2920
Simulator.
The Simulator can be used to test the actual operation
of the 2920 prograrp. For example, the first step of such
a test might be
to specify an input waveform; such as a
sweeping sinusoid
for a filter application, which will test
the
performance of the filter over different frequencies.
• Establish Objectives
• DeSign
Block Diagram • Translate Functional
Blocks
Into Program
Blocks
• 2920 Assembler
(Intellec®Senes II)
• Signal Processor
Appllcallons
Soltware/Compller
If a problem occurs, i.e., unexpected or erroneous out-
put, the debugging tools of the Simulator can be called
into
action to test variables at different points of the
2920 program.
If a program change is needed, it can be implemented
immediately within the Simulator, by directly changing
the
contents of the program through the Intellec system
keyboard.
The revised program is then tested anew.
Every
parameter of the 2920's operations can be tested,
changed, traced,
or stored on diskette files for later
analysis
or documentation .
• SimUlator
• Test Program
• System Debug
• Evaluate
System
Performance
• Program EPROM
(Intellec®)
• UPP 103
• 2920
Personality
Card
• DeSign
Venllcallon
Figure 1-1. 2920 Design Sequence
Table 1-3. Development System Provides Computer Aided DeSign Contrast
Between Discrete Component
and 2920 DeSign Methodologies
Task Discrete Component 2920 Approach 2920 Benefits
1.
Specify Product
Develop Block Diagram Develop Block Diagram Same starting point
2. Develop
Prototype A. Design Circuits A. Translate block Reduce
2-3 weeks to 2-3
B. Design Breadboard diagram into program days
C. Build Breadboard
B.
Use Signal Processing
-Locate parts Applications
Software/Compiler
-Put together C. Assemble program
3. Troubleshoot prototype A.
Input signal Via Simulator Use classic troubleshooting
B. Observe output with scope A. Specify input signal techniques
on interactive
and DVM
or Spectrum B. Observe output and terminal
Analyzer RAM contents
4. Correct Errors A. Replace
Component A. Edit and assemble Reduce 3 degrees of error to
B. Redesign layout program
1; save time
C. Redesign circuit B. Go back to 3
D.
Go back to 3
5. Documentation Write down observation
data, Data recorded on develop- Accuracy increases;
and write report ment system in an easy to Time savings
follow report
1-3

INTRODUCTION AND TERMINOLOGY
When the simulation indicates the program is operating
to specifications, it can be stored on a diskette. The
latest version
can then be loaded into the 2920 device for
testing in the
hardware prototype.
Figure
1-1 outlines the development sequence for a 2920
design. There are several important points to note that
makes the 2920 much more efficient for a system design:
1) With the 2920, hardwired analog functions are now
implemented with flexible software,
2) Instead of designing circuits for each of the building
blocks of the block diagram, a sequence of 2920
instructions are used to implement each of the
blocks,
3) Instead of building hardware prototypes early in the
design phase of the product development, the 2920
uses a computer-aided design and debug package to
facilitate design and development, and
4) There is no need for a hardware prototype until
such a time that the system has been simulated and
found to be completely functional and meets design
specifications.
Table 1-3 shows the contrast in design methodologies
for a 2920 design and one using analog components.
Numerous benefits derive from using the 2920 develop-
ment system for signal processing design
and implemen-
tation. The digital methodology, with its unique tools
(see Chapters 3 and 9) to aid designing and debugging,
helps to:
a) standardize the design process, and
b) allow for immediate changes. Thus it can
c) reduce drastically the time needed for creating new
products or for modifying prior work to fix errors
or to add new features.
1.3 Benefits of the 2920 Signal
Processor Approach
The 2920 is a solution for many signal processing needs.
It is a complete system in a single 28-pin package. Along
with 2920 are all the design and development tools
required to move a product idea into finished product.
The 2920 uses a digital sampled data system approach
for signal processing applications. The digital sampled
data approach brings many attributes to signal process-
ing. Table 1-4 summarizes some of these benefits.
1.3.1 2920 Device Benefits
Lower manufacturing cost for 2920-based products
results from a lower
part count, improved reliability,
1-4
and the elimination of costly preCiSion components.
Also eliminated is the production re-tuning or 'tweak-
ing' so often required in analog systems integration.
The flexibility for rapid design changes in prototypes
is
a direct result of the 2920's programmability. Alter-
native designs are readily compared by reprogramming
the 2920's EPROM. The re-use of standard debugged
program blocks facilitates the creation of alternatives in
both existing and future products.
The digital approach provides inherently stable, predic-
table, and reproducible results. The NMOS integrated
circuitry means increased reliability. Conceptual errors
or inefficient implementation choices are easily found
during debugging
and performance evaluation using the
2920 Simulator. The performance you design for is the
realized performance.
Savings in long-term product maintenance, support,
and enhancement result from the relative ease with
which engineering changes are implemented in software.
Field maintenance
is reduced by digital stability and LSI
reliability.
1.3.2 Deveiopment-Support-Tool Benefits
Long term savings in large
part are derived from the
2920 support package. The 2920 Signal Processing
Applications Software/Compiler (SPAS-20) contains
very powerful code generation
and macro capabilities,
plus graphics
and analysis capabilities permitting inter-
active specification and adjustment of design param-
eters. Creating usable libraries of macros and signal
processing routines means ever increasing productivity
due to building on the successes of the past.
The 2920 Assembler creates the actual machine bit pat-
terns to be programmed into the 2920. Its careful error
analysis detects problem areas, and the debugging
information it provides greatly facilitates design evalua-
tion during simulation.
The 2920 Simulator permits execution of any part of a
2920 program, plus collection of trace data on variables.
This tool bears a strong family resemblance to Intel's
In-Circuit-Emulators (ICE). The analysis and evalua-
tion capabilities inherent in the 2920 Simulator make
possible rapid problem isolation in the field or in the
factory. It can also be used to generate revised object
code for a quick check
on proposed fixes or enhance-
ments. This revised code can be saved and used to pro-
gram the 2920.

J.
2.
3.
4.
5.
6.
7.
8.
INTRODUCTION AND TERMINOLOGY
Table 1-4. 2920 Benefits
Discrete Analog Components
Board full of components
Component matching: select, test, combine, match,
tune, test
Production-lot variation in circuit performance
Performance degradation over time, signal degradation,
due to circuit interaction or noise
Discrete
component tolerances prohibit exact matching
of multi-pole frequency
Time-consuming fixes
to problems with hardwired
design
Costly
components for accuracy
Custom designs are costly, risky, and require or create
heavy
commitments
1-5
Intel 2920 Signal Processor Methodology
Single chip
System tweaking eliminated because
performance from
device to device is identical: digital processing is stable,
predictable,
and repeatable
Digital accuracy
is repeatable
Eliminated-the 2920 restricts degradation of signal
quality to the instants
at which signal samples are
digitized and converted back to analog
Restriction eliminated because digital realizations are
not subject to such tolerances
Quick
program changes
Not needed because their functions can be created in
software
Programming permits vastly greater flexibility for
modifications, improvements, and
extra features;
Much wider range
of options at reduced costs, size,
weight
and maintenance.

Sampled Data Systems 2

CHAPTER 2
SAMPLED
DATA SYSTEMS
2:0 SAMPLED DATA SYSTEMS
Sampled data systems can be implemented using either
analog
or digital processing techniques, or both. Figure
2-1 shows two different types of sampled data systems:
sampled analog system and sampled analog/digital
system. Examples
of sampled analog systems include
transversal filters using CCD or bucket brigade shift
registers analog weighted-taps and switched capacitor
techniques to implement a filter characteristic. The
identical systems can also be implemented using digital
instead
of analog processing. Such systems are referred
to as digital sampled data systems. This type of system
can be implemented with the 2920 Signal Processor.
This chapter will discuss the various elements that com-
prise a digital sampled data system and also look at the
design considerations in representing a continuous
analog signal with digital sampled
data techniques.
2.1 Elements of a Digital Sampled Data
System
The block diagram shown in Figure 2-2 illustrates the
basic blocks
of a general purpose sampled data system
using a digital signal processor. In this configuration it
is assumed that both the input and output signals are
analog. This is not a necessary condition since digital
signals can be considered a special type of analog signals
and processed accordingly. Elements of the block
diagram are discussed below.
The system in Figure 2-2 operates
on the input analog
signal using the indicated components in sequence:
• Anti-Aliasing Filter-This filter is used to bandlimit
the incoming analog signal prior to sampling; thus a
continuous analog filter is used. This minimizes
possible distortion terms (aliasing noise) which
could arise from signal frequencies that are too high
relative to the sample rate (Section 2-2).
• Input Sample and Hold (S&H)- The filtered input
signal
is then sampled at a fixed rate determined by
the digital processor. Each resulting sampled
amplitude
is held long enough for subsequent pro-
cessing (such as analog-to-digital conversion).
2-1
Analog-to-Digital Converter (A/D)-The held
analog voltage
is converted to a digital word. This
digital word then represents the sampled input
signal voltage. (Since the processor must operate on
individual digital words, it is necessary to
characterize the continuous analog
input signal by
discrete digital words which retain the information
of the original signal.)
• Digital Processor-Each digitized sample is now
processed by the digital processor, which has been
programmed to
perform a predetermined algo-
rithm. Typically, a general microprocessor can be
programmed to
perform any funciton, but the
resulting execution time is too limiting for most
analog applications. The 2920 eliminates this pro-
blem because its architecture
is configured to take
advantage of serial repetitive signal processing,
while at the same time preserving many of the
advantages of the general purpose microprocessor.
Digital-to-Analog Converter
(D/ A)-The pro-
cessed digital words are converted back to analog
using the
D/ A. Again, the analog signal is approx-
imated by discrete amplitude levels (as in the A/D).
In addition, the D/ A sampled output weights the
signal
output in the frequency domain by sin(x)/x,
thereby causing some signal distortion (Section
2-2).
• Output Sample-and-Hold (S&H)-One method of
reducing the output frequency distortion is to widen
the sin(x)/x rolloff by resampling the output signal
using a very narrow sample width. The S&H takes
the
D/ A held output and res ampies it with narrow
pulses.
Another use of an output S&H is to store
values when several outputs are multiplexed during
a single sample period.
• Reconstruction Filter-Since the desired output
signal is a continuous representation of the pro-
cessed input signal, it is necessary to remove high
frequency components resulting from the
D/ A or
sample-and-hold outputs. This, in effect, smooths
the analog
output from sample to sample. A
lowpass filter is used to perform the signal
"reconstruction". This filter can also be used to
compensate for the sin(x)/x frequency rolloff of the
D/ A or S&H (Section 2-2).

SAMPLED DATA SYSTEMS
C) SAMPLED ANALOG/DIGITAL SYSTEM
Figure 2·1. Sampled Data System
Figure 2·2. Elements of a Sampled Data System
2.2 Effects of Sampling
Assuming an input spectrum F(jw) and a sampling fre-
quency fs, the
output spectrum for square-topped
sampling
Fst (jw) is found to be
FST (jw) =.2.... sin (wtl2)
T wtl2
L F [j(w-nws)]
n=-oo
From this equation, the gain is a continuous function of
frequency defined by ~ SIn Jt~y2) where T is the sample
pulse width, t
is time, T the sample period, and w the
frequency in radians per second.
The time-and-frequency-domain plots for the square-
topped sampled signals are shown in Figure 2-3. Figure
2-3a and 2-3b show the signal before and
after sam-
pling. The corresponding spectra are shown in Figure
2-3c and 2-3d respectively. Figure 2-3d is a plot of the
above equations where multiple spectra are formed
around mUltiples of the sample frequency. As long as
2-2
the adjacent spectra do not overlay excessively (aliasing
distortion), the
continuous signal can be represented by
discrete samples
at that sampling frequency.
The quality
of representation of a continuous signal by
the sampled and digitized signal is determined by several
factors: a) sampling rate b) sampling pulse width
c) sampling stability and d) digitizing accuracy. The cor-
responding distortion terms are: a) aliasing noise b)
signal reconstruction noise
c) jitter noise and d) quan-
tization noise respectively. These four factors can cause
unacceptable distortion if they are
not chosen properly.
By properly designing the sampled data system, these
distortion or noise terms can be made insignificantly
small, so that the sampled data system closely represents
the analog equivalent system.
The sampled data system implementation will have the
added advantages of digital processing and software
flexibility. The following sections will discuss these
sources
of imprecision.
a lnput~slgnal waveform
b Square-topped sampled signal
FREQUENCY
c Input-signal spectrum
{T--;;;;t2
D.. - __
~
::E
..:
~.... -- .... --
t'""""t •
d Square-topped sampled-signal spectrum
Figure 2·3. Analysis of Sampled Signal

SAMPLED DATA SYSTEMS
2.2.1 Aliasing Noise
A sampling theorem relating the minimum required
sampling frequency
to the signal bandwidth can be
stated as follows: if a signal f(t), a real function
of time,
is sampled instantaneously at regular intervals, at a rate
higher than twice the signal bandwidth, then the
sampled signal contains all the significant information
of the original signal. This would then define the
minimum sampling frequency required. In practice, a
sampling rate
of 3 to 4 times the 3dB bandwidth of the
input signal
is not uncommom.
Figure 2-4 shows the effects
of sampling rate on the
separation
of sampled signal spectra. When the sample
rate
is r~duced, the adjacent spectra overlaps. The
TIME DOMAIN
AM'~'C7L
TIME
A·'I~LLL:/
TIME
A·'I~
TIME
A.')
~
TIME
overlapped spectral energy cannot be separated from
the desired signal
and so a distortion is caused called
aliasing noise.
Figure 2-4 shows the effect of sample rate
on aliasing
noise for a given input signal. Note the
amount of
overlap increases as the sampling frequency is decreased
for a fixed input signal bandwidth. Similarly, for a fixed
sampling frequency, the overlap could be reduced by
increasing the frequency. The overlap couJd also be
reduced by increasing the frequency rolloff
of the input
signal by using anti-aliasing filters prior to sampling.
Figure
2-5 illustrates the overlap for several types of
popular anti-aliasing filters. These tradeoffs between
filter selectivity and sampling frequency are
part of the
design process with sampled data systems. Such trade-
offs are discussed more fully
in later chapters.
FREQUENCY DOMAIN
A.' I
~
FREQ
A.' I
f. FREQ
AMP
f.
FREQ
A·'IZ!.
\ •
FREQ
Figure 2-4. Effects of Sampling Rate on Aliasing Noise
2-3

SAMPLED DATA SYSTEMS
10
20
30
40
1/21s
FREQUENCY
o 0 3 POLE BWRTH
.0 3POLEO 3dBTCH
A 0 5 POLE BWRTH
.. 0 5POLEO 3dBTCH
c 0 7 POLE BWRTH
• 0 7POLEO 3dBTCH
Is
Figure 2·5. Effects of Filtering on Aliasing Noise
2.2.2 Signal Reconstruction Distortion
Signal reconstruction is the process that extracts the
desired signal from the periodic output samples which
have been formed
after digital processing.
DIGITAL
INPUT
D/A
The intention is to convert the signal, which has been
sampled and held after digital processing, back to
analog form with a minimum loss of information. The
output of a sample-and-hold circuit (S&H) or a digital-
to-analog converter (DIA) has a frequency spectrum as
shown in Figure 2-6 where the sample width T
is equal to
the period
of the sample T. The amplitude gain factor
has a noticeable
rolloff within the signal bandwidth
when that bandwidth approaches half the sampling fre-
quency. Unless it is compensated for, this distortion of
the input signal will cause loss of information similar to
the loss from a lowpass filter with insufficient band-
width. Table
2-1 lists the rolloff in dB as a function of
the sample width T and the signal bandwidth B.
To correct this situation, either the reconstruction
sampling pulse width should be made narrow relative to
one over the signal bandwidth (1/B), or a sin(x)/x cor-
rection should be applied in the
output filter.
Figure 2-6b shows the effect of resampling with a nar-
rower pulse. The amount of signal energy contained in
the narrower sampling pulses declines by an amount
proportional to the duty cycle TIT. It may be necessary
to compensate for this gain loss when analyzing the
relative effects of fixed offsets, overshoot, ringing, and
other spurious signals that degrade the desired signal.
ANALOG
OUTPUT
·1
L S&H
~ ___ ----I,",~I RECO~~L~~~CTION
'- _____ -" (8) ""-- _____ .... (C)
.;
(A)
AM'I~
LLJ
..
TIME
AMP
I.
FREO
AM'I n
n Dr-.
(8)
DODD
TIME
AM' t
~"
I.
FREO
AM'p~//
(C)
-------
RECONSTRUCTION
AMP ,
,/FILTER
,"
"
I.
FREO
..
TIME
Figure 2-6. Analog Signal Reconstruction
2-4

SAMPLED DATA SYSTEMS
When the data samples have been established, they are
passed through a reconstruction lowpass filter whose
primary purpose is to remove the higher-frequency spec-
tra caused by the
output sampling (Figure 2-6c). It can
also help shape the
amplitude and phase response of the
output network.
Table 2-1. Reconstruction Distortion Due to
Sample Pulse Width
BT
-20 log sin
nBT
---
nBT
dB
0.1
0.14
0.2 0.58
0.3 1.32
0.4 2.40
0.5 3.92
0.6 5.96
0.7 8.70
0.8 12.60
0.9 19.3
1.0
00
2.2.3 Jitter Noise
The information content of a signal is carried in some
combination of its amplitude, phase, or frequency.
Noise is introduced by any process that alters the infor-
mation carried to the degree that the signal cannot be
restored to its original condition. An ideal sampling
process assumes that ideal samples are taken at periodic
intervals, i.e.,
that the amplitude of each sample is
exactly equal to the value of the signal at the time of the
sample. If the sampling waveform is not stable, then the
signal will be sampled at times other than what was
expected with an error corresponding to the rate of
change of the sampled signal.
The jitter noise can be estimated by examining a
sinusoidal input signal that is sampled with average
period T and a peak-to-peak deviation of the period 2T
(Figure 2-7). Using sin(wti) as the value of the sinusoid
exactly at the i-th sampling instant, and sin (W(tj+T
j»as
the value
at the actual sampling instant, where Ti is the
time error at that point, then the error or jitter noise at ti
is the difference between the exact and the sampled
values of the signal voltage, i.e.,
NJ(t.) = sin(wtl) - sir,(wti+ WT
I)
= (l-COS(WT) * sin(wt) + sin(wTi) *cos(wt)
11-- } .... I-----NOISE VARIATION--- __
SAMPLE JITTER~::II -
11111111
11111111
I-T±T_/
/_2T
TIME
Figure 2-7. Sampling Jitter
The noise power is simply the sum of the squares of its
quadrature components
NJ2 = [1 -cos (WT)] 2 +sin2(WT)
= 2 - 2COS(WT
I)
Assuming that the timing errors are independent from
sample
to sample and uniformly distributed between ±T,
the expected noise power is
2-5
T
E{N/ }= ;T f 2-2 cos (WT
I)
dTI
=2-2
sin WT
WT
For wt <TI12, a Taylor series expansion of sin(wt) yields
an approximation for the mean square noise power of