KLINGER KSCICGB User manual

847-336-7556
www.unitedsci.com
1
CAVENDISH GRAVITATIONAL BALANCE
CGB001
DESCRIPTION OF THE INSTRUMENT
The CGB001 Cavendish Gravitational Balance is a miniature version of the apparatus
used by Henry Cavendish in 1797-8 to measure the density of the Earth. The experiment
allows the value of the gravitational constant, G, to be measured, although Cavendish
did not use his version for that purpose. The experiment is remarkable for the ability to
measure an extremely tiny force using simple mechanical means.
The apparatus contains a pendulum system (1, Figure 1) consisting of an adjustable
suspended central rod carrying a small mirror for the optical lever detection system, a
light aluminum cross-piece with two 20g lead balls 10 cm apart, and a light damping
vane. The pendulum is mounted in a massive aluminum housing (2). Two large 1.5 kg
plastic-coated lead balls (4) rest atop light aluminum cylinders on a swivel (4) that enables
the balls to be swung from one side to the other of the apparatus. They can also be
placed onto two circular sliding mounts (6) that allow the distance between the pendulum
and the attracting masses to be varied. The base rests on three leveling feet (6).
An oil reservoir and damping oil (7) as well as a damping magnet (8) are provided.
1
4
2 3
5
Figure 1
3 7
6 8
www.KlingerScientic.com
Cavendish Gravitational Balance KSCICGB

847-336-7556
www.unitedsci.com
2
SPECIFICATIONS
IDENTIFICATION OF THE COMPONENTS
1. Upper suspension rod locknut
2. Pendulum angle adjustment block
3. Suspension rod height adjusting nut
4. Angle indicator disk
5. Angle scale disk
6. Suspension rod locking screw (1 of 2)
7. Upper suspension rod
8. Torsion filament
9. Glass cover plate (1 of 2)
10. Torsion filament connector plate
11. Balance centering plate (2 halves)
12. Concave mirror for light pointer
13. Balance lock actuating screw
14. Balance lock mechanism
15. Small lead ball (1 of 2)
16. Damping oil trough
17. Balance damping vane
18 Aluminum body
19. Swinging support for large lead balls
20. Scale (on base—1 of 2)
21. Base plate
22. Leveling nut (1 of 3)
23. Foot (1 of 3)
24. Sliding ball support (1 of 2)
25. Ball support cylinder (1 of 2)
26. Large lead attracting ball (1 of 2)
27. Damping oil supply tube
28. Damping oil reservoir support
29. Reservoir support set screw
30. Reservoir clip tightening screw
31. Reservoir support clip
32. Damping oil reservoir
33. Balance locking rod
34. Lower suspension rod
Figure 1
www.KlingerScientic.com

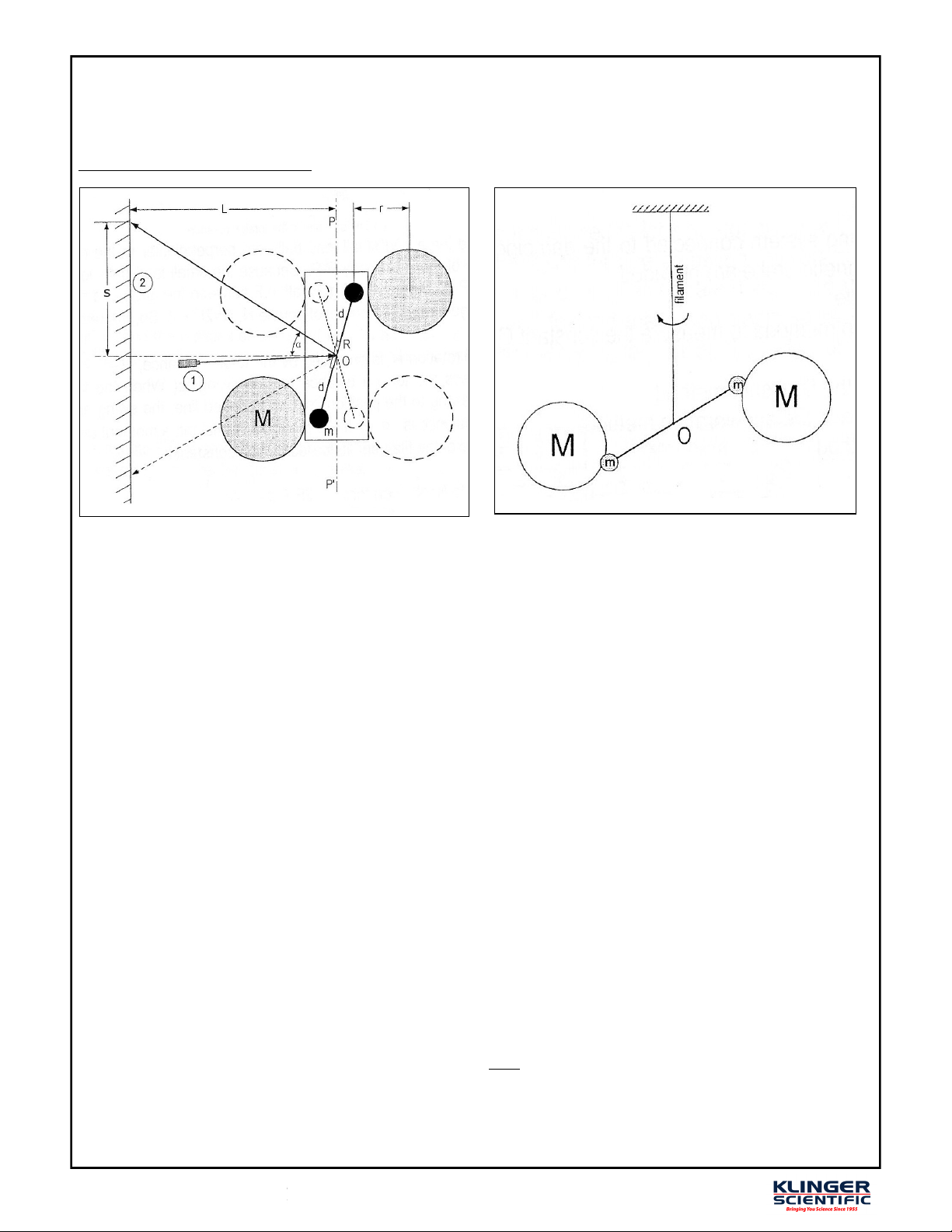
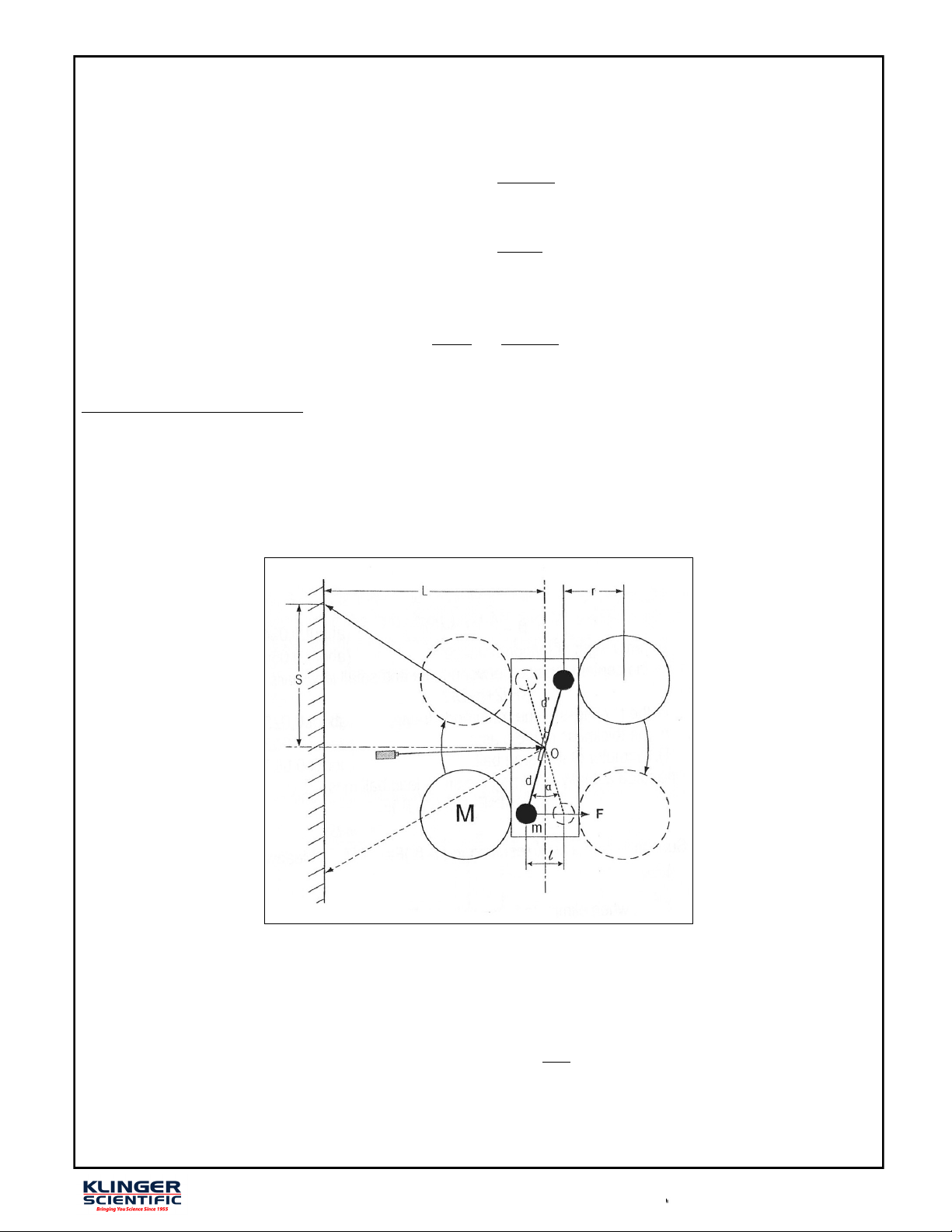
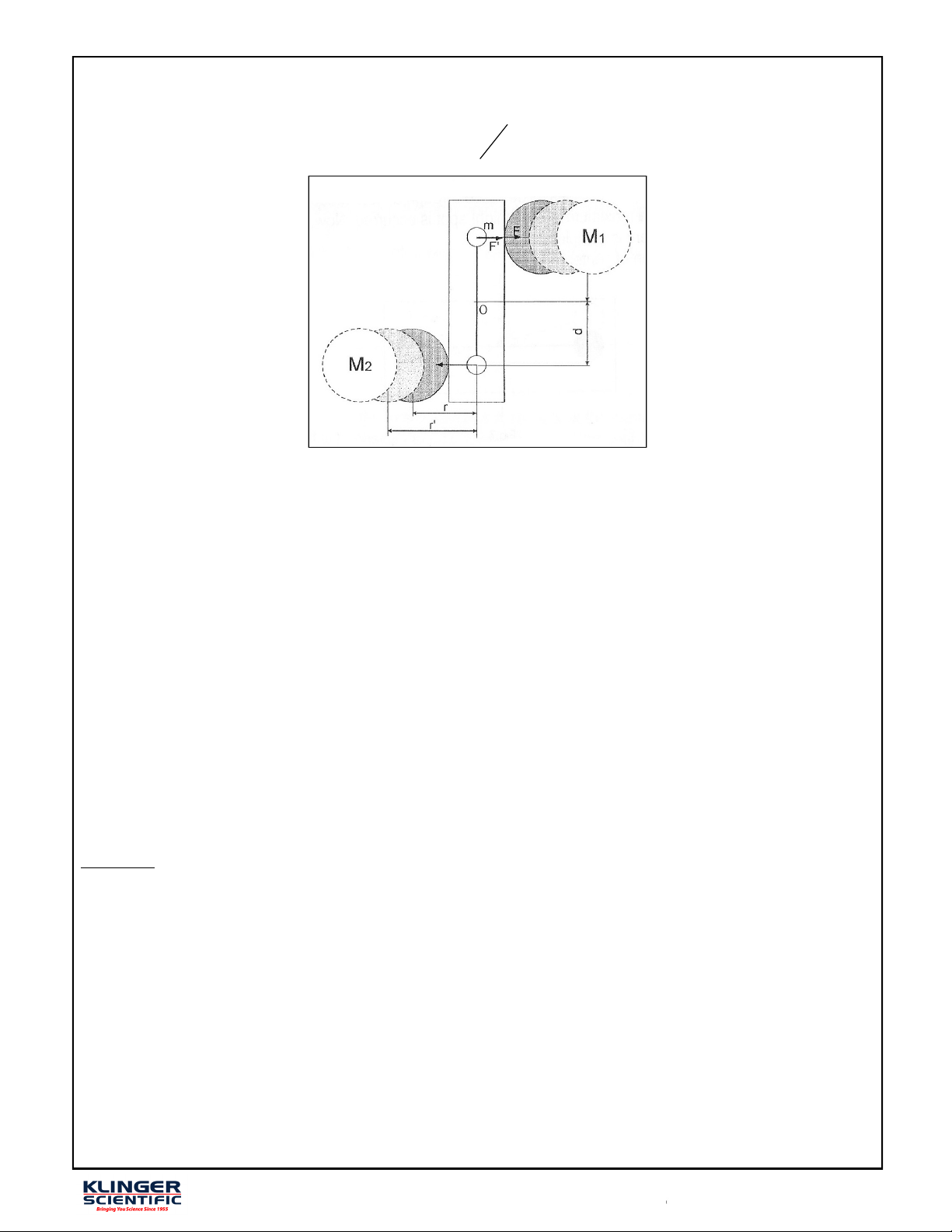
847-336-7556
www.unitedsci.com
3
The torsion balance is housed in a solid aluminum main body (18) with glass win-
dows (9) on both sides to eliminate drafts.
The adjusting nut (3) on the top can be used to raise or lower the upper suspension rod
(7) in order to adjust the vertical position of the balance. The angle adjustment block
(2), angle indicator disk (4) and the circular scale (5) are used to read the angle the
balance is rotated from its equilibrium position. The locking screws (6) on the upper
side of the body can fix the upper suspension rod in its angular equilibrium position.
The filament (8), 150mm long and made of beryllium bronze, has connector plates (10)
at each end and connects the upper and lower suspension rods (7,34). A concave mirror
(12) with 2m focal length is mounted on the lower suspension rod. Under the mirror
are the locking rod, a pair of lead balls of 10.0mm diameter (15) and the damping vane
(17), which projects into in a damping trough (16).
The locking screw (13) on the side can raise or lower the locking mechanism
(14).With the locking mechanism lowered, the balance is suspended on the filament
and can rotate freely. When the mechanism is raised, it lifts the balance by the locking
rod (33) and presses the arm of the balance against the body, removing the load from
the filament and immobilizing the balance.
The filament is extremely delicate and the load of the balance stresses it highly. The
balance should only be released and allowed to swing freely when an experiment is in
progress. At all other times, the balance should be locked to preserve the filament.
The main body is mounted on an aluminum base (21). The three leveling screws (22)
under the base are used to level the device. The two grooves on the base serve as
guides for the sliding ball supports (24). The ball support cylinders (25) for the large
lead balls (26) rest on the sliding blocks. The distance between the large balls can be
measured by the scales (20) along the grooves.
The oil damping system is mounted on one side of the base and connected to the
damping chamber (16) through a tube (27).
Mass of large lead balls: Approximately 1.5kg
Difference between the two balls < 0.002kg
Mass of small lead balls: Approximately 0.02kg
Difference between the two balls <0.0005kg
Arm length of the torsion balance: 5.0x10-2m
Torsion Filament: Length: approximately 150mm
Cross sectional area: 0.145±0.08mm2
Material: Be-Sn-Cu alloy
Period of the torsion balance 590±10sec.
Scale: 140mm with 1mm divisions
Full-scale error < 0.1mm.
Damping method: Silicone oil
Relative error of Gravitational Constant: < 15%
Operating temperature: 10 –40°C
Relative humidity: < 40%
Operating location: Should be free from vibration, sunlight,
radiant heat, magnetic and electric fields
Dimensions: 300x300x420mm
Net weight: 12kg
www.KlingerScientic.com

847-336-7556
www.unitedsci.com
4
THEORY
The most common methods used to measure the value of the gravitational constant are
the displacement method and the acceleration method.
The Displacement Method
The displacement method is named after the final angular displacement of the torsion
balance to be measured in the experiment. In Figure 2, the torsion balance is set up a
large distance Lfrom a wall or screen with a millimeter scale 

. The concave mirror is
illuminated by a laser 

, producing a spot of light on the scale. The distance between
the small lead balls, each of mass m, and the axis O is d. The concave mirror is
mounted at the center of the arms connecting the two small balls. The projection system
produces a large displacement of the light spot, s, for a small angular displacement of
the mirror, /2. This allows the user to measure the angle  easily, and determine the
angular displacement of the mirror from the central position, /2.
Two large lead balls of same mass Mare placed against the glass windows of the main
body, symmetric to the axis O. Figure 3 illustrates the side view of the arrangement.
The line connecting the centers of the large and small balls is perpendicular to the center
line of the main body, PP’. Figure 2 greatly exaggerates the angles of the balance
for clarity; the deviation of the balance from its central position is extremely small,
so the centers of the small balls are almost on the line PP’, and the torque produced
by the gravitational force Fbetween the large and small balls, N, is given by 2F·d.
When the torsion balance comes to rest, the restoring torque applied by the torsion
filament, N’ is k·/2, where the coefficient k represents the torque in the wire when it is
twisted by 1 degree. Since N = N’, we have 2F·d= k·/2. Therefore
(1)
If we now move the large lead balls to their symmetrically opposite final positions, indicated
by the large dotted circles in Figure 2, the torsion balance will be subjected to a torque
in the opposite direction and will move to the new equilibrium position represented by
Figure 2 Figure 3






d kF 4

www.KlingerScientic.com

847-336-7556
www.unitedsci.com
5
the dotted line and small circles in Figure 2. Its angle of rotation to the new equilibrium
position can be determined by the displacement S(=2s) of the projected dot on the
scale. The distance from the mirror to the screen being L, and S « L, we have
= S/2L (2)
The torque constant of the wire, k, can be determined from the balance’s period of
oscillation T , using
derived from the harmonic motion equation
where the moment of inertia Iis given by
the moments of inertia of the lower suspension rod, mirror, and balance crossbar are
neglected, since they are extremely small compared with those of the lead balls.
Hence the torque constant of the wire kcan be expressed as
(3)
Substituting expressions (2 ) and (3) into (1), we have
(4)
The gravitational force between the large ball Mand the small ball mat a
separation of ris
(5)
Combining expressions (4) and (5) to eliminate F, we have the formula for the gravitational
constant G:
(6)
Where ris the distance between the centers of the large and small balls, dthe length of
the arm of the torsion balance, Sthe maximum displacement of the light dot, Mthe
mass of the large lead balls, Tthe period of oscillation of the balance, and Lthe distance
from the mirror to the scale.
Strictly speaking, distance rbetween the balls in Figure 2 should be
However, the error caused by the approximation will not exceed 2% so that it can be
neglected.
k
T1 2
 


k
dt
d
I
2
2
 
 iii mddmdmrmI 2
2
22
2
11
22
2
2
2
2
284
T
md
T
I
k  
LT
mdS
L
S
T
md
dd
k
F
2
2
2
22
2
8
4
1
4

























2
r
Mm
GF 
LMT
dSr
G
2
22


L
dS
rdrr 42 "








www.KlingerScientic.com

847-336-7556
www.unitedsci.com
6
There is a second, more important correction, illustrated by Figure 4. The small ball m
is subjected not only to the force Fapplied by the large ball M1, but also to a force f
applied by the large ball M2. Therefore, the value for Gobtained from expression (6)
needs to be corrected.
In Figure 4, the distance between mand M2is
But and so,
(7)
If the component of f in the opposite direction to Fis f’, then
(8)
Substituting expression (7) into expression (8), we have
where
(approx. 0.074)
Here dis the arm length of the torsion balance (0.05m), and rthe distance between
the centers of the large and small balls, which can be determined from
Where His the thickness of the main body (approx. 0.025m), hthe thickness of the
glass window (approx. 0.002m), and D the diameter of the large ball (approx. 0.0635m).
Figure 4
22
4dr 
2
r
Mm
GF 
21
MM 
F
dr
r
dr
Mm
Gf 


















22
2
22
44
22
4
'
dr
r
ff  
 
F
dr
r
F
dr
r
dr
r
Ff 























2
3
22
3
22
22
2
4
4
4
'
 
2
3
22
3
4dr
r



22
D
h
H
r
www.KlingerScientic.com

847-336-7556
www.unitedsci.com
7
The force actually acting on the small ball is
Substituting this into expression (4), we have
Since
the corrected expression for Gis
(9)
The Acceleration Method
The acceleration method determines the value of Gfrom the acceleration produced by
the gravitational force.
As in the case of final displacement method, the large balls are first moved to the positions
against the glass windows and when the small balls have come to rest, the torque
produced by the gravitational force will balance the torque in the wire due to the rotation.
When the large balls are now moved to the dotted position shown in Figure 5, the initial
force on the small ball F’ will be the sum of the gravitational force Fand the elastic
restoring force, f. Therefore, we have
(10)
The small ball moves a small distance lunder F’. The motion can be regarded as a
uniformly accelerated over the first short period of time (within 90 seconds). Therefore
 
FFFfF   1'
 
LT
mdS
F2
2
1



2
r
Mm
GF 


















LMT
dSr
G
2
22
1
1


Figure 5
2
22'
r
Mm
GFfFF 
www.KlingerScientic.com

847-336-7556
www.unitedsci.com
8
we can apply Newton’s Law
where ais the acceleration.
Substituting into (10), we have
(11)
Expression (11) can be corrected to take into account the gravitational force applied by
the second large ball:
(12)
If the distance traveled by the small ball is l, we have
In order to solve this equation for a, we need to find the distance lthat the small ball
has traveled in the first tseconds after the large ball was moved into the dotted
position (Figure 5).
From Figure 5 we have
Therefore
So the acceleration acan be determined from
(13)
Substituting (13) into (12), we have
The acceleration method is simpler than the displacement method. However, although
it requires 1—2 hours to stabilize the instrument in its initial position, this is still only
half the time required for the two stabilizations needed in the displacement method.
Also, the error in the Gvalue obtained by the acceleration method is usually larger.
The Inverse Proportion Verification
The apparatus allows the separation of the small and large balls to be varied by
supporting the large balls on two light aluminum cylinders (24 & 25 in Figure 1) that
slide in grooves on the instrument base. This method can be used to verify the relation
between the gravitational force and the distance between the objects:
From expression (4)
maF'
M
ar
Mm
Fr
G22
22

 
M
ar
G2 1
2
 
2
2
1atl
d
l
L
S2

2
2
1
2at L
dS
l
Lt
Sd
a
2

 
2
2
2
1
MLt
Sdr
G

2
1
r
F
LT
mdS
F
2
2


www.KlingerScientic.com

847-336-7556
www.unitedsci.com
9
therefore
So the relationship between F and r will be verified if we can show experimentally that
Figure 6 illustrates the change in the distance rbetween the large and small balls.
Record the displacement S of the light dot and the corresponding distance rthen plot
1/r2vs. S on graph paper to verify that the relationship between F and 1/r2is linear.
Since each small ball is also subjected to the force of the second large ball, the Svalues
obtained above will be too small and need to be corrected by replacing Swith (1+
 )S.
SETUP
The experiments described in this manual require the following accessories:
 Laser (He-Ne or diode) and support material
 Stopwatch (electronic or mechanical, 1/100 s)
 3m tape measure
 Screen and support material
 Vernier caliper
 Balance (2000g capacity x at least 1g resolution)
 Calculator.
Leveling
 Choose a location as free of vibration as possible and place the instrument on a
solid, level surface.
 Set up the laser and the screen as indicated in Figure 2
 Measure and record the masses of the large lead balls.
 Gently turn the locking knob (16, Figure 1) counter-clockwise to unlock the torsion
balance so that it hangs free on the suspension filament.
NOTE: The suspension filament is extremely delicate and is highly stressed when
bearing the load of the torsion balance. Avoid sudden or jerky movements when
releasing or locking the balance.
 Use the adjusting nut (3) to center the small balls vertically in their cutouts in the
main body.
 Adjust the position of the laser so that the light beam is incident at the center of the
mirror and reflects onto the screen.
SF 
2
1
r
S
Figure 6
www.KlingerScientic.com

847-336-7556
www.unitedsci.com
10
 Use the leveling screws (22) to adjust the angle of the apparatus so that the lower
suspension rod (34) hangs in the center of the hole in the balance centering plate
(11).
 Apply torsion to the filament using the angle adjustment block (2) until the small
balls just touch the glass window, then finely adjust the leveling screws for the largest
displacement of the light dot on the screen. Then return the angle adjustment block
to its original position.
Centering
In equilibrium, the torsion balance should be centered as shown by the black balance in
Figure 7. Otherwise the user should do the following:
 Determine the equilibrium position: Let the torsion balance oscillate with a large
amplitude so that the small balls touch the glass windows. Mark the two end posi-
tions of the light beam on the screen and connect them with a straight line. The
center of the line will be the desired equilibrium position of the balance, x.
 Confirm the equilibrium position: Use the damping magnet to reduce the amplitude
of the swing. (The lead balls are diamagnetic and experience a weak repulsive force
near the pole of a magnet. Applying this force alternately to each lead ball as it
passes the center point of the swing will reduce the swing amplitude) Then record
the end positions of the light dot on the screen as shown in Figure 8.
 The equilibrium position xcan be calculated as follows. For the damped motion we have:
or
Figure 7
Figure 8
k
xx
xx
xx
xx 





2
3
1
2
'
'
'
'
312
31
2
2
2
'
xxx
xxx
x


www.KlingerScientic.com