PASCO ME-9430 User manual

Instruction Manual
012-14781A
Plunger Cart
ME-9430
800-772-8700 www.pasco.com
Features
Accessories
Please see the PASCO catalog or the PASCO web site at
www.pasco.com
for information about accessories such as tracks, springs,
bumpers, pulleys, masses, and special attachments that
are designed to be used with the Plunger Cart.
Introduction
The Plunger Cart is a 500 gram cart with an aluminum body
and ABS (acrylonitrile butadiene styrene) end caps. It has a
spring plunger in one end and magnets in the other. It has
“hook-and-loop” (Velcro®) tabs on the plunger end for
inelastic collision studies. The magnets can be used for
elastic collisions studies. The spring plunger has three set-
ting positions and is released by a plunger trigger on the
top of the plunger end of the Plunger Cart. Both ends of the
Plunger Cart have convenient tie points at the top and the
bottom. On the top of the Plunger Cart is an accessory tray
3.
1.
9.
8.
2.
4.
5.
6.
7.
9.
10.
4.
1Low-friction Retractable Ball-Bearing Wheels 6 Two Mounting Holes
2ABS End Caps 7 Accessory Tray
3Magnets in non-plunger end cap (not shown) 8 Plunger Trigger
4Upper Tie Point (each end cap) 9 Hook and Loop (Velcro®) Tabs
5Slot for Cart Picket Fence (ME-9804) 10 Lower Tie Point (each end cap)

Plunger Cart Usage
2
012-14781A
that can hold extra masses. The tray has threaded holes
for attaching PASCO accessories such as a Cart Adapter
that can be used to mount a Motion Sensor, and slots for
holding a Cart Picket Fence.
Other Features
The Plunger Cart has ball-bearing wheels that are
designed with narrow edges to minimize friction. The cart
has a spring suspension system that prevents damage to
the wheels and internal components if the cart is dropped
or stepped on. Plunger Carts can be stacked for easy stor-
age.
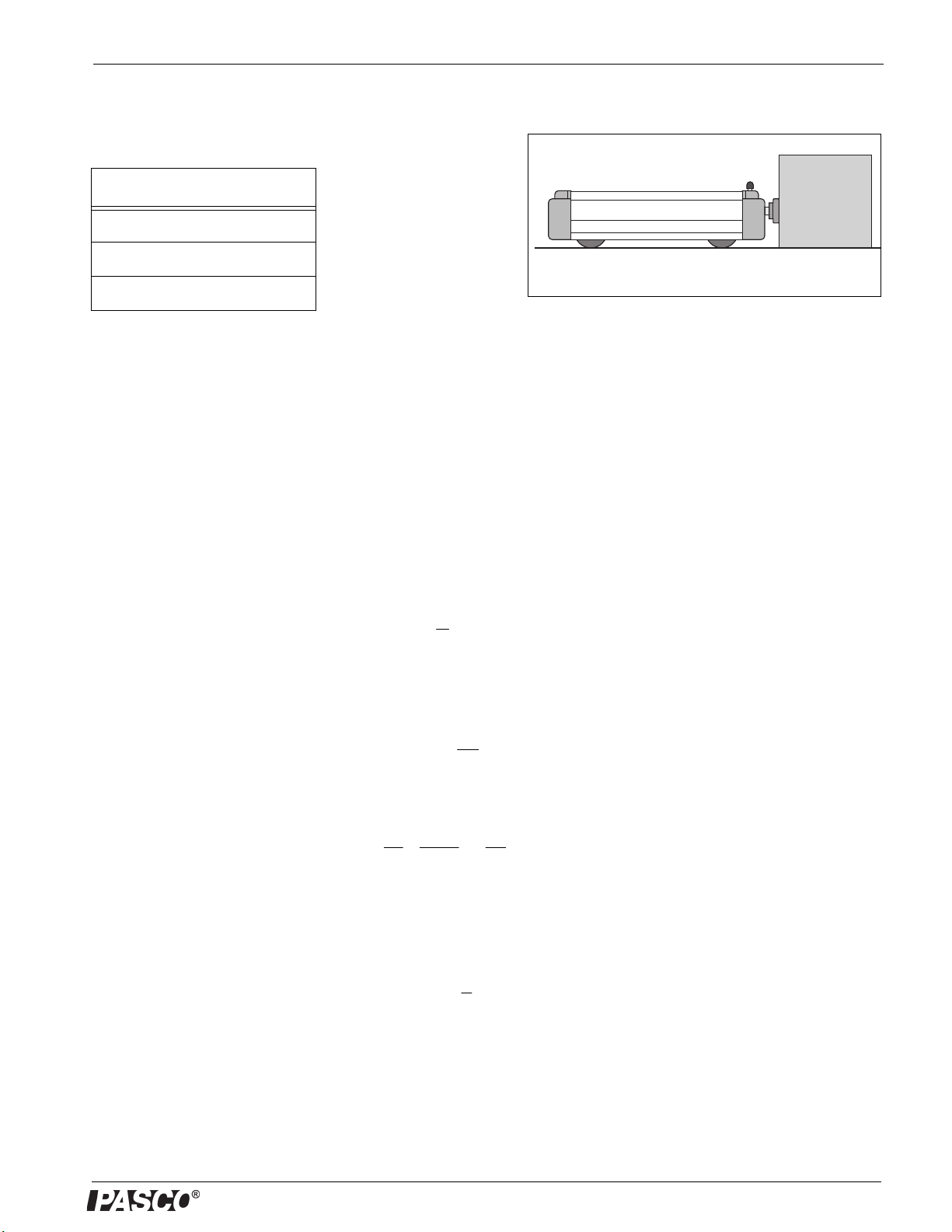
Plunger Operation
The plunger has three indentations on the top side that you
can see when the plunger is fully extended. Inside the cart
is a Retention Bar located above the plunger. When the
plunger is pushed in far enough so that an indentation lines
up with the Retention Bar, the plunger will be held in that
position until the Plunger Trigger is pushed down. If the end
of the plunger is next to an object such as a heavy book,
the Plunger Cart will accelerate away from the object when
the Plunger Trigger is pushed down and the plunger
applies a force.
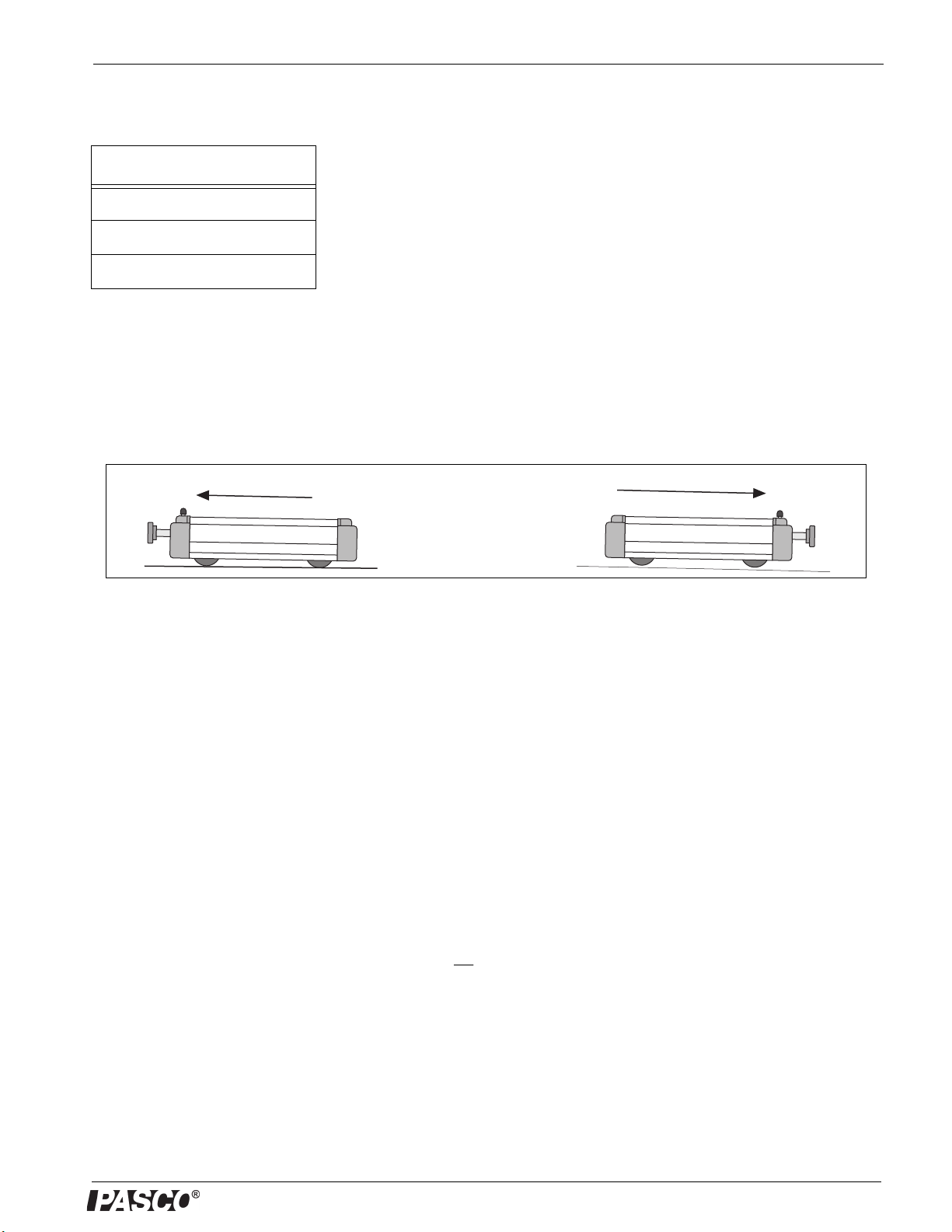
Positions #1 and #2
Apply a slight upward force on the end of the plunger, Push
the plunger into the Plunger Cart until you hear or feel the
first “click” (Position #1) as the indentation on the plunger
lines up with the Retention Bar. Lower the end of the
plunger slightly to disengage it from the Retention Bar, and
push the plunger a little farther into the Plunger Cart.
Slightly raise the end of the plunger and push the plunger
until you hear or feel the second “click” (Position #2). To
release the plunger, push down on the Plunger Trigger.
CAUTION: The plunger comes out rapidly, so be prepared.
For example, do not hold the plunger end of the Plunger
Cart against your eye (or anything else that would be
harmed) if the plunger is released.
Position #3
Apply a slight upward force on the end of the plunger. Push
the plunger all the way into the Plunger Cart until the Posi-
tion #3 indentation catches on the Retention Bar. The end
of the plunger will be flush with the end cap of the Plunger
Cart. The plunger pushes outward with maximum force
when it is released from Position #3. This is also the posi-
tion used when doing inelastic collisions with the Velcro
bumpers.
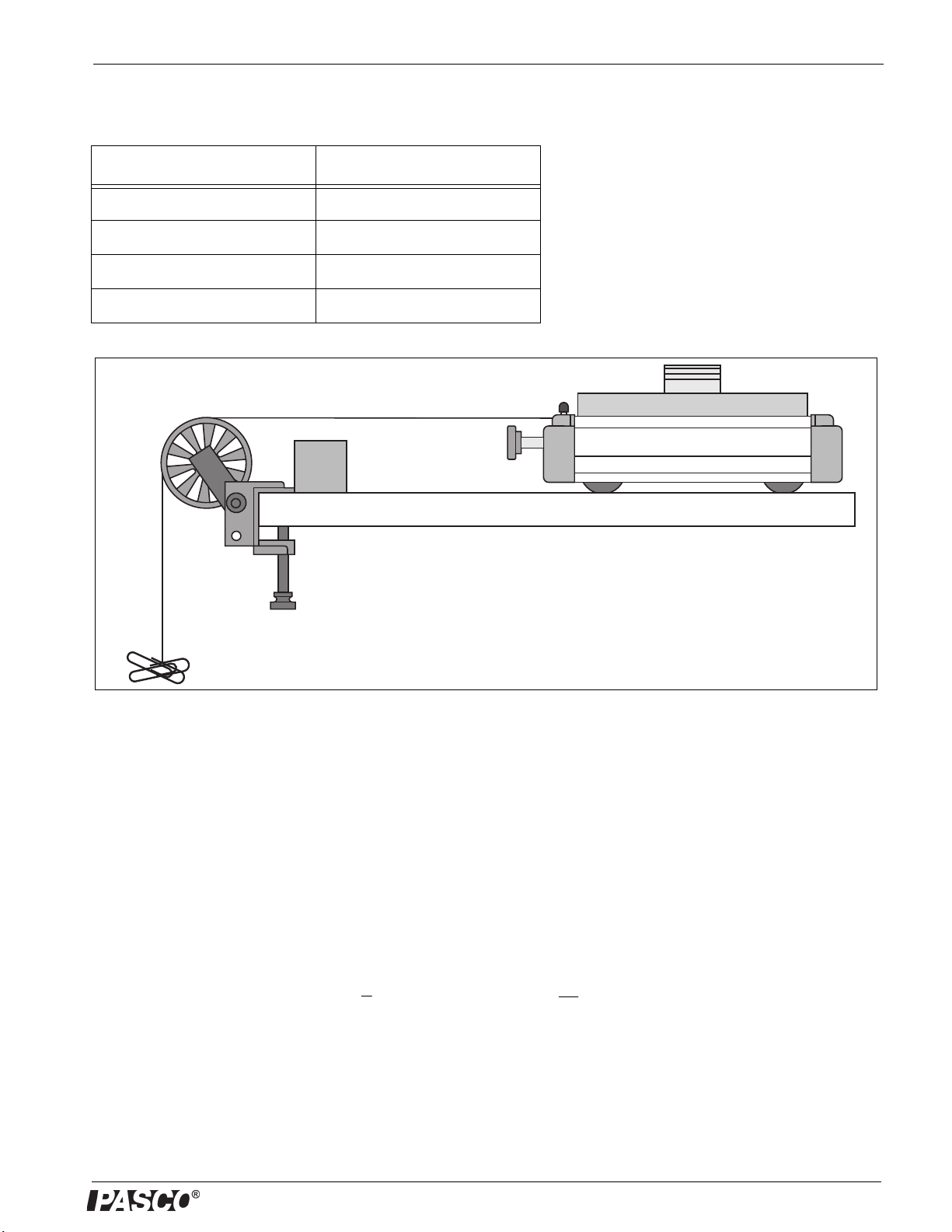
Usage
The following illustrations show a few of the ways that the
Plunger Cart is used. See the PASCO web site at
www.pasco.com for more information.
Collision Cart
The PASCO ME-9454 Collision Cart is a “twin” of the
Plunger Cart but it is red and does not have a spring
plunger. The different colors make it easier to keep track of
the carts in collisions studies.
Plunger Cart Dynamics Systems
Plunger Carts are included in bundles with tracks, adjust-
able feet, end stops, a track pivot clamp a friction block,
and other accessories such as mass bars, springs, photo-
gate brackets, “cart picket fences”, and a pulley with clamp.
.
Plunger Trigger
Approximate Position of
Plunger Retention Bar
Position #1
Position #2
Position #3

Plunger Cart Technical Support
3
012-14781A
Brackets and Bumpers
There are a variety of accessories that fit onto a Plunger
Cart or onto a track for use with a Plunger Cart.
Experiments
The included Plunger Cart experiments rely on the mea-
surement of time, distance, and mass. The basic equip-
ment required is: stopwatch, metric tape measure (2 m or
more), and a mass balance.
For information about the suggested equipment and other
items for use with the Plunger Cart, see the PASCO cata-
log or the PASCO web site at
www.pasco.com
Technical Support
For assistance with any PASCO product, contact PASCO
at:
More Information
For more information about the latest revision of this
Instruction Manual, visit:
www.pasco.com/manuals
and enter the Product Number.
For information about the Plunger Carts or any PASCO
product, what software to use, and what other accessories
are available, check the PASCO web site.
Smart
Gate
Photogate Bracket
Pulley with
Clamp
Braided
Physics String
Force Sensor Bracket
Force
Sensor
Motion SensorBracket
Elastic Bumper
Equipment Suggested Model Number
Cart Masses, 250 g (2) ME-6567A
Friction Block ME-9807
Stopwatch ME-1234
Pulley with Clamp ME-9448B
Hooked Mass Set SE-8959
Physics String SE-8050
Triple-Beam Balance SE-8723
Meter Stick SE-8827
30 Meter Measuring Tape SE-8712A
Address: PASCO scientific
10101 Foothills Blvd.
Roseville, CA 95747-7100
Phone: [phone] (worldwide)
800-772-8700 (U.S.)
Web: www.pasco.com
Email: [email protected]

Plunger Cart Appendix
4
012-14781A
Warranty, Copyright, and Trademarks
Limited Warranty For a description of the product warranty, see the PASCO catalog. Copyright The PASCO scientific 012-14781A Instruction
Manual
is copyrighted with all rights reserved. Permission is granted to non-profit educational institutions for reproduction of any part of this manual,
providing the reproductions are used only in their laboratories and classrooms, and are not sold for profit. Reproduction under any other circumstances,
without the written consent of PASCO scientific, is prohibited. Trademarks PASCO and PASCO scientific are trademarks or registered trademarks of
PASCO scientific, in the United States and/or in other countries. All other brands, products, or service names are or may be trademarks or service marks
of, and are used to identify, products or services of, their respective owners. For more information visit www.pasco.com/legal.
Appendix
Replacing the Wheel-Axle Assemblies (PASCO ME-6957A - set of four)
Warning! When the baseplate is removed, the wheel-axle assemblies may pop upward because they are supported on
compressed springs. Pull the baseplate with one hand and cover the wheel-axle area with the other hand. This will help
keep the wheel-axle assembly from popping out.
1. Using a Phillips screwdriver, remove the screws from the
non-plunger end cap.
NOTE: The screws that connect the end cap to the body of
the Plunger Cart are thread-forming screws and may require
substantial force to remove and reinstall. A #1 Phillips point
screwdriver is recommended.
2. Position the Plunger Cart with the baseplate facing
upward.
3. Begin to slide the baseplate out of the cart. Be careful to
“catch” each wheel-axle assembly as it is uncovered.
4. With the car in a stable position, lift the wheel-axle
assemblies from the grooves.
NOTE: Be sure to keep the components such as springs,
plunger, and magnets in their proper orientation. Rearranging
or moving any items could change the operational capability
of the Plunger Cart.
5. Place the new wheel-axle assemblies over the suspen-
sion springs.
6. Push the rear axle down against the springs first, and
slide the baseplate back into a position that covers the
wheel-axle assembly.
7. Push the front axle down second, and slide the baseplate
all the way back into its original position.
8. Replace the non-plunger end cap with the two screws.
Thread-forming Screw
End Cap
Wheel-Axle Assembly
Baseplate
Compression
Spring

Experiments Plunger Cart
012-14781A 5
Experment 1: Kinematics (Average vs. Instantaneous Velocities)
Purpose
In this lab, the Plunger Cart will be used to investigate one dimensional accelerated motion. The
Plunger Cart will be launched over the floor using the built-in spring plunger. The Plunger Cart will
“decelerate” over the floor under the combined action of rolling friction and floor slope. You will be
able to establish whether or not the acceleration of the Plunger Cart is constant. This will be done
by initially assuming a constant acceleration and then by examining the results to see if they are
consistent with this assumption.
Theory
The cart will be allowed to roll to a stop. The distance D covered and the total elapsed time T from
launch to stop will be measured and recorded. The average velocity over this interval is given by
the following equation:
If the acceleration of the cart is constant as it rolls to a stop over the floor, then the initial instantaneous
velocity of the Plunger Cart at the final moment of launch is given by the following equation:
And the value of the acceleration would be given by the following equation:
If the acceleration and vo are known, then the time t1 required to cover the distance d to some
intermediate point (i.e. short of the final stopping point!) can be calculated by applying the quadratic
formula to the following equation:
Calculated values of t1 will be compared with directly measured values. The extent to which the
calculated values agree with the directly measured values is an indication of the constancy of the
acceleration of the cart.
Note your theoretical values in Table 1.1.
Equipment Needed
Plunger Cart
Metric Tape Measure
Stopwatch
Figure 1.1
av
D
v
T

Eqn. 1
0av
2D
v2v
T

Eqn. 2
Eqn. 3
0
2
0v
v2D
atT
T


 
Eqn. 4
2
01 1
1
dvt at
2


Plunger Cart Experiments
6012-14781A
Procedure
1. Once you have roughly determined the range of the Plunger Cart, clearly mark a distance d that is
about half way out from the start. Measure this distance and record it at the top of Table 1.1.
2. Using a stopwatch with a lap timer and metric tape, it is possible to determine t1, T and D for each
launch. Practice this step a few times before you start recording data.
NOTE: To eliminate reaction time errors, it is very important to have the person who launches the
Plunger Cart also be the timer!
3. Launch the cart and record the data described in the previous step for six trials. To cock the spring
plunger, push the plunger in, and then push the plunger slightly upward to allow one of the notches
on the plunger bar to “catch” on the edge of the small metal bar at the top of the hole. (Don’t count
the trials in which the timer feels that a distraction interfered with the measurement.) Record your
best trials in Table 1.1.
4. Using the equations described in the theory section and the data recorded in the table, do the
calculations needed to complete the table.
Data Analysis
d= _________ cm
Table 1.1
Questions
1. Is there a systematic difference between the experimental and calculated values of t1? If so, suggest
possible factors that would account for this difference.
2. Can you think of a simple follow up experiment that would allow you to determine how much the
cart’s “deceleration” was affected by floor slope?
Trial
Experiment Theory
% Diff.
t1 (s) T (s) D (cm) v0 (cm/s) a (cm/s2)t1 (s)
1
2
3
4
5
6

Experiments Plunger Cart
012-14781A 7
Experiment 2: Coefficient of Friction
Purpose
In this lab, the Plunger Cart will be launched over the floor using the on-board spring launcher. The
cart will “decelerate” over the floor under the combined action of rolling friction and the average
floor slope. To determine both the coefficient of rolling friction µr and , the small angle at which the
floor is inclined, two separate experiments must be done. (Recall that to determine the value of two
unknowns, you must have two equations.)
Theory
The cart will be launched several times in one direction, and then it will be launched several times
along the same course, but in the opposite direction. For example, if the first few runs are toward
the east, then the next few runs will be toward the west. See Figure 2.1. In the direction which is
slightly downslope, the acceleration of the Plunger Cart is given by the following equation:
And the acceleration in the direction that is slightly upslope will be:
Numerical values for these accelerations can be determined by measuring both the distance d that
the cart rolls before stopping and the corresponding time t. Given these values, the acceleration
can be determined from the following equation:
Having obtained numerical values for a1 and a2, Eqn. 1 and Eqn. 2 can be simultaneously solved
for
µ
r
and  .
Equipment Needed
Plunger Cart
Metric Tape Measure
Stopwatch
Figure 2.1
UPSLOPE DOWNSLOPE
1r
agsin g


 
Eqn. 1
2r
agsin g


 
Eqn. 2
2
2d
a
t

Eqn. 3

Plunger Cart Experiments
8012-14781A
Procedure
1. Place the Plunger Cart in its starting position and then launch it. To cock the spring plunger, push
the plunger in, and then push the plunger slight upward to allow one of the notches on the plunger
bar to “catch” on the bar inside the cart. Using a stopwatch and metric tape, determine the range d
and the total time spent rolling t. Record these in Table 2.1.
2. Repeat step 1 six times for each direction and enter your results in Table 2.1.
3. Using Eqn. 3, compute the accelerations corresponding to your data and an average acceleration
for each of the two directions.
4. Using the results of step 3, determine
µ
r
and  by algebraically solving for the two unknowns.
Table 2.1
Average Acceleration = ___________ cm/s2 Average Acceleration = ___________ cm/s2
Data Analysis
Coefficient of rolling friction = ________________ Floor Angle = ________________
Questions
1. Can you think of another way to determine the acceleration of the Plunger Cart? If you have time, try it!
2. How large is the effect of floor slope compared to that of rolling friction?
First Direction Second Direction
Trial d (cm) t (s) a (cm/s2)Trial d (cm) t (s) a (cm/s2)
11
22
33
44
55
66

Experiments Plunger Cart
012-14781A 9
Experiment 3: Newton’s Second Law (Predicting Accelerations)
Purpose
In this lab, a small mass m will be connected to the cart by a string as shown in Figure 3.1. The
string will pass over a pulley at the table’s edge so that as the mass falls the cart will be accelerated
over the table’s surface. As long as the string is not too elastic and there is no slack in it, both the
falling mass and the Plunger Cart will have the same acceleration. The resulting acceleration of this
system will be experimentally determined and this value will be compared to the acceleration
predicted by Newton’s Second Law.
Theory
The cart will be released from rest and allowed to accelerate over a distance d. Using a stopwatch,
you will determine how long it takes, on average, for the cart to move through the distance d. An
experimental value for the cart’s acceleration a can be determined from:
Assuming that the tabletop is truly horizontal (i.e. level), Newton’s Second Law (F = ma) predicts
that the acceleration of this system will be:
Equipment Needed
Plunger Cart Pulley and Pulley Clamp
Mass Set Balance
Stopwatch String
Paper clips Block (to act as bumper)
Bumper Block
Paper clips Figure 3.1
2
2d
a
t

2
1
dat
2

which leads to (Experimental Value)

Plunger Cart Experiments
10 012-14781A
Procedure
1. Set up the pulley, cart, and a bumper of some sort to prevent the cart from hitting the pulley at the
end of its run. Add the following masses to the accessory tray of the Plunger Cart: 10-g, 50-g, 500-g,
and two 20-g masses.
2. Carefully level the table until the cart has no particular tendency to drift or accelerate in either
direction along its run.
3. Tie one end of the string to the tie point on the top of one end of the Plunger Cart. Drape the string
over the pulley. Adjust the pulley up-or-down so the string is level.
4. Adjust the length of the string so that the longest arrangement of masses that you intend to use will
not hit the floor before the cart has reached the end of its run. Put a loop in this end of the string.
NOTE: The Plunger Cart’s acceleration falls to zero when the falling mass hits the floor.
5. Hang enough paper clips onto the dangling loop in the string until the cart will just continue to move
without apparent acceleration when barely nudged. This small added mass will compensate for
friction in the system and will be ignored in the following calculations. The paper clips will remain
attached to the loop throughout the experiment!
6. Move a 10 gram mass from the bed of the Plunger Cart to the hanging loop and pull the cart back
to a clearly marked starting point. Determine the distance d that the Plunger Cart will move from
the starting point to the bumper block and record this distance at the top of Table 3.1.
NOTE: The total mass of the system will remain constant throughout the experiment.
7. Practice releasing the cart being careful not to give it any push or pull as you do so. The best way
to do this is to press your finger into the table in front of the Plunger Cart thereby blocking its
movement. Quickly pull your finger away in the direction that the cart wants to move. At the instant
you pull your finger away, start your stopwatch. Stop your stopwatch at the instant the Plunger Cart
arrives at the bumper. To eliminate reaction time errors, it is best that the person who releases the
cart also does the timing!
8. Determine the average time for the cart to move through the distance d, having been released from
rest. Record the average of the four time trials in which you have the most confidence in Table 3.1.
Repeat for all of the masses given in the data table.
9. Excluding the pulley, determine the total mass of your system, Mtotal (Plunger Cart, added masses,
string) and record at the top of Table 3.1. (It will be close to 1100 grams, but you should check it
on a balance.)
10. Fill in the table using your data and the equations given in the Theory section.
Data Analysis
d = _________________ cm Mtotal = _________________ gram
net
total
F
aM 
or (Theoretical. Value)
total
m
ag
M






Experiments Plunger Cart
012-14781A 11
Table 3.1
Question
1. Can you think of any systematic errors that would effect your results? Explain how each would skew
your results.
Trial m (g) Average
time (s) aexp (cm/s2)a
th (cm/s2)% Diff.
110
220
330
440
550
660
770
880

Plunger Cart Experiments
12 012-14781A
NOTES

Experiments Plunger Cart
012-14781A 13
Experiment 4: Cart Calibration (Measuring the Spring Constant)
Purpose
The Plunger Cart has a spring plunger, which can be used for producing relatively elastic collisions
and providing a reproducible launch velocity.
Theory
For this and the following experiments, it will be necessary to find the spring constant k of the cart’s
spring plunger. As compressional forces F are applied to the spring, the spring will compress a
distance x, which is measured with respect to its uncompressed equilibrium position. If F is plotted
versus x on graph paper, the spring constant is given by the slope of the graph as:
Once k is known, it is possible to predict the launch velocity vo by using conservation of energy,
since the elastic potential energy stored in the spring is converted into kinetic energy at the time of
launch. The launch velocity can be found from:
which leads to:
This predicted launch velocity can be experimentally checked by measuring the total rolling distance
d on a horizontal surface and the corresponding time t for given launch conditions. This leads to:
It is assumed that the acceleration of the Plunger Cart is constant, so that the initial velocity of the
cart at the moment of launch is twice the average velocity of the cart over its whole run.
Equipment Needed
Plunger Cart Stopwatch
Mass Set Balance
Pan for holding masses Metric Ruler
Metric Measuring Tape
F
k
x



Eqn. 1
22
00
11
mv kx
22

Eqn. 2
Eqn. 3
00
k
vx
m

0
d
v2
t

Eqn. 4

Plunger Cart Experiments
14 012-14781A
Procedure
1. Stand the Plunger Cart on its end so that the spring plunger is aimed up, as shown in Figure 4.1.
Using masking tape or rubber bands, fix a ruler to the car and adjust it so that the 0 cm mark on
the ruler lines up with the upper surface of the plunger. Take care to avoid parallax errors!
2. Carefully add enough mass to the top of the plunger so that it is nearly fully depressed. Record this
mass and the corresponding compression x (initial position) of the spring in Table 4.1.
3. Remove approximately one quarter of the mass used in step 2. Record the new mass and x values
in Table 4.1.
4. Repeat step 3 until no mass remains on the plunger.
5. Plot a graph of F versus x using your data and determine the slope of the best line through your
data points. This slope is the spring constant for your car. Show your slope calculations on the graph
and record k below.
6. Determine the mass of the cart using a mass balance and record this value below.
7. Using Eqn. 3 and your values for m, xo (i.e. the compression of the cocked spring) and k, predict
the launch velocity of your cart and record this below.
8. Cock the spring plunger to the value of xo that you have chosen, then place the cart in its starting
position and launch it. Using a stopwatch and a meter stick, determine the average range d and
the average total time spent rolling t. Record these below.
NOTE: To avoid reaction time errors, the person who launches the cart should also time the cart’s
motion.
9. Using Eqn. 4, determine the observed value of vo and compare it with the predicted value.
Total added mass
Pan for holding masses
Note the initial position
of the plunger
15 cm ruler attached
to the Plunger Cart
1/2 total added mass Note the final position
of the plunger
Note the new position
of the plunger
123
Figure 4.1

Experiments Plunger Cart
012-14781A 15
Data and Analysis
mass of cart = ________________ kg
k = ________________ N/m xo = _______________ m
Predicted value of launch velocity v0 = _______________ m/s
Average d = ____________________m Average t = ________________ s
Observed value of the launch velocity v0 = _________________ m/s
Percent difference (% Diff) between observed and expected values of v0 = _________
Table 4.1
Trial m (kg) F (= mg) N x (m)
1
2
3
4
5
6
7
8

Plunger Cart Experiments
16 012-14781A
NOTES

Experiments Plunger Cart
012-14781A 17
Experiment 5: Rackets, Bats, and "Sweet Spots"
Purpose
When a batter or tennis player strikes a ball, a portion of the rotational kinetic energy of the bat or
racket is transferred to the ball. In a somewhat oversimplified picture, the motion of the bat or racket
can be thought of as a simple rotation about a pivot which is located near its end and close to the
batter’s wrists. The portion of the bat’s original kinetic energy that is transferred to the ball depends
on the distance y between the point of impact and the pivot point. The position on the bat
corresponding to the maximum energy transfer is called a “sweetspot”. We will call this maximum
energy sweetspot SS1.
NOTE: For simplicity, it is assumed that the collisions are perfectly elastic.
Theory
As any batter can tell you,
if you hit the ball at a cer-
tain point on the bat, there
will be no shock, or
impulse, transferred to
your hands! This
“sweetspot” is generally
located at a different posi-
tion than SS1 and is called
the “percussion point”. We
will call this zero impulse
sweetspot SS2. For a
given “bat” and pivot, the
position of SS2 can be
found from:
where I is the rotational inertia of the bat for the corresponding pivot, m is the total mass of the bat,
and ycm is the distance from the pivot to the center of mass of the bat. (e.g. If a uniform rod of length
L is pivoted about an endpoint, SS2 is located at 0.67L from the pivot.)
The positions of both SS1 and SS2 can be found theoretically, or by using the Sweet Spot computer
program (see page 20 for details). The position of SS2 can be found experimentally using the
PASCO Force Sensor or, roughly, by actually hitting a ball at a variety of positions on the bat and
noting where the least shock to your wrists occurs. In this experiment, a method for determining
the location of SS1 is described.
If you have already done the experiment to determine the coefficient of rolling friction for your cart
for the same surface that you are using in this experiment, you can determine the kinetic energy of
the cart at the moment after impact as shown in Eqn. 2.
Equipment Needed
Plunger Cart Metric Measuring Tape
Meter Stick or Long Rod Mass Set
y
x
Figure 5.1
Pivot Point
Eqn. 1
SS2
cm
I
y
my


Plunger Cart Experiments
18 012-14781A
Procedure
1. Set up the system as shown in Figure 5.1. Position the cart so that its plunger hangs over the edge
of the table several centimeters.
NOTE: You will need a long, horizontal table, or board for this experiment. A 3/4 inch by 1 foot by
8 foot plywood board is recommended.
2. Arrange to have a stop of some sort to insure that you always use the same pullback angle for the
hanging meter stick.
3. Pull the meter stick or rod back to the pullback angle that you have chosen and release it, allowing
it to strike the cart plunger. Record the corresponding values of y and x in Table 5.1.
4. Repeat step 3 four times for each value of y, changing it from roughly 10 to 90 cm in 10 cm increments.
5. Compute the average value of x for each value of y.
6. By interpolation, determine the location of SS1 from your data and record it below Table 5.1.
7. Using Eqn. 1, compute the location of SS2 and record it below Table 5.1.
8. If time permits, repeat the above after either repositioning the pivot (i.e. “choking up”) or adding 100
grams or so at some point on the stick.
NOTE: This would add a little realism to the experiment since neither a bat nor a tennis racket is
uniform!
Table 5.1
y-position of SS1 = _________ cm y-position of SS2 = _________ cm
Questions
1. Is it possible to construct a “Superbat” for which both SS1 and SS2 coincide? If so, what changes
would have to occur to the uniform rod to bring SS1 and SS2 closer together? (You might use the
SweetSpot computer program to help you answer this!)
2. What assumptions have we made in analyzing this system? How do they affect our results?
Trial y (cm) x (cm) Average x
(cm)
Optional µmgx
(joules)
1 10 ________ ________ ________ ________
2 20 ________ ________ ________ ________
3 30 ________ ________ ________ ________
4 40 ________ ________ ________ ________
5 50 ________ ________ ________ ________
6 60 ________ ________ ________ ________
7 70 ________ ________ ________ ________
8 80 ________ ________ ________ ________
2
1mv mgx
2
 
Eqn. 2

Experiments Plunger Cart
012-14781A 19
"Sweet Spot" Computer Program
The following is a listing of the "Sweet Spot" computer program written by Scott K. Perry of American River College,
Sacrament, CA, using Quickbasic 4.5.
PRINT “Y-Impact (m)”; TAB(16); “Cart-Speed
(m/s)”; TAB(35); “Omega (rad/sec)”;
TAB(54); “Impulse at Pivot (Nsec)”
COLOR 15
PRINT
FOR k = 1 TO 9
r = k / 10
a = Mc / 2 + (Mc  r) ^ 2 / (2  I)
b = –Mc  Wo  r
c = –PE + (1 / 2)  I  Wo ^ 2
v = (–b + SQR(b ^ 2 – 4  a  c)) / (2  a)
w = (I  Wo – Mc  r  v) / I
Delt a P = M c  v + M s  w  L / 2 – Ms  Wo  L / 2
v = INT(1000  v + .5) / 1000
w = INT(1000  w + .5) / 1000
DeltaP = INT(100  DeltaP + .5) / 100
PRINT TAB(5); r; TAB(20); v; TAB(39); w;
TAB(60); DeltaP
NEXT
PRINT: PRINT
INPUT “Would you like to input different values
”; a$
IF a$ < > “N” and a$ < > “n” GOTO Begin
END
REM Program: SWEET SPOTS and PER-
CUSSION POINTS (Fixed Pivot)
REM (Version: 15DEC91)
CLS
LOCATE 1, 1
INPUT “What pullback angle will you be
using for this experiment (deg.)”; theta
INPUT “What is the mass of your meter-stick
’bat’ (kg); Ms
g = 9.8: Mc = .5: L = 1: theta = theta / 57.3
COLOR 15
Begin:
CLS
LOCATE 1, 1
INPUT “How far from the center-of-mass is
the pivot located (m)”; S
INPUT “How large is the load mass (kg)”; m
IF m = 0 GOTO Skip
INPUT “ How far is the load mass from the
pivot (m)”; y
Skip:
I = (1 / 12)  Ms  L ^ 2 + Ms  S ^ 2 + m  y ^ 2
PE = (Ms  S + m  y)  (1 – COS(theta))  g
Wo = SQR(2  PE / I)
h = (1 + 2  (y / L)  (m / Ms))  (1 –
COS(theta))  L / 2
PRINT: PRINT
COLOR 14

Plunger Cart Experiments
20 012-14781A
NOTES