Sartorius 2405 User guide
Other Sartorius Scale manuals

Sartorius
Sartorius PMA.Economy User manual

Sartorius
Sartorius LP Models User manual

Sartorius
Sartorius EVO1Y User manual

Sartorius
Sartorius Signum 1 User manual

Sartorius
Sartorius EC1XS.-......-L Original instructions

Sartorius
Sartorius SECURA3101-1CEU User manual

Sartorius
Sartorius IS16EDE-H User manual

Sartorius
Sartorius ME215 User manual

Sartorius
Sartorius Master Pro Series User manual
Sartorius
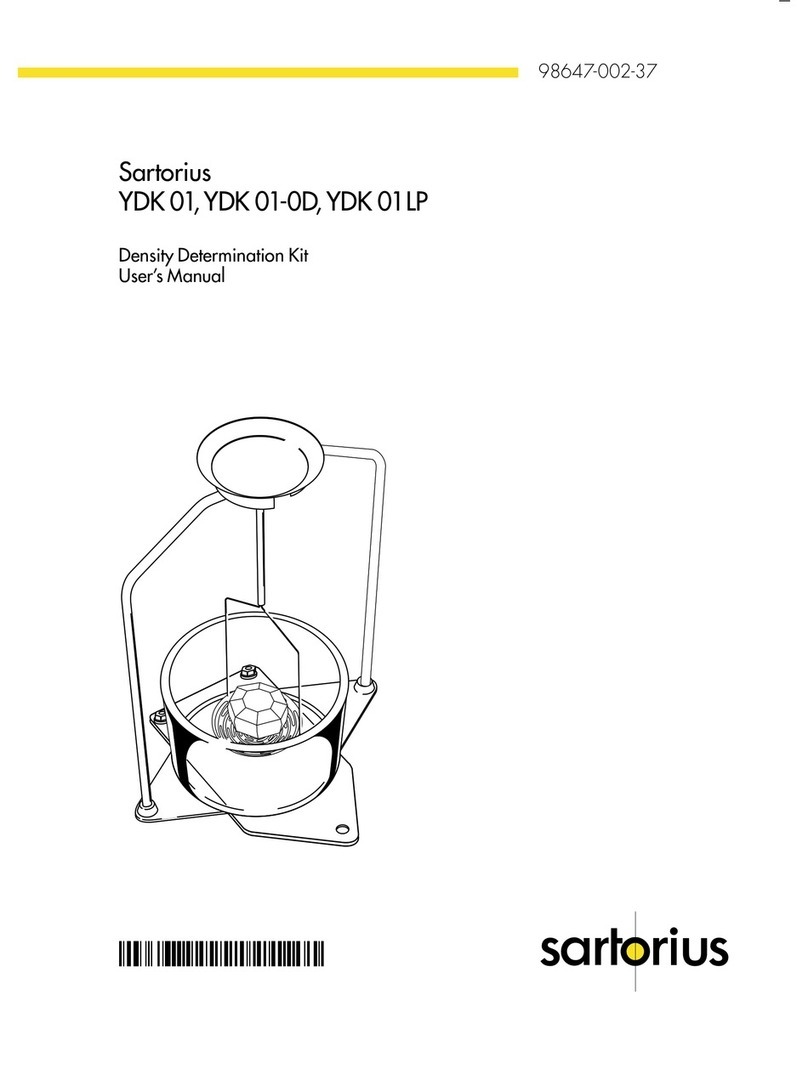
Sartorius YDK 01 User manual

Sartorius
Sartorius MC 210 S User manual

Sartorius
Sartorius YDS01SQP User manual

Sartorius
Sartorius BL150S User manual

Sartorius
Sartorius Entris II Specification sheet

Sartorius
Sartorius Secura User manual

Sartorius
Sartorius Cubis MCA Series User manual

Sartorius
Sartorius PMA 35D User manual

Sartorius
Sartorius PMA 7501-000G User manual

Sartorius
Sartorius Factory Series Original instructions

Sartorius
Sartorius Secura User manual