3B SCIENTIFIC PHYSICS 1002956 User manual

6
Operating instructions
3B SCIENTIFIC3B SCIENTIFIC
3B SCIENTIFIC3B SCIENTIFIC
3B SCIENTIFIC® PHYSICSPHYSICS
PHYSICSPHYSICS
PHYSICS
The torsion pendulum may be used to investigate free,
forced and chaotic oscillations with various degrees of
damping.
Experiment topics:
•Free rotary oscillations at various degrees of damp-
ing (oscillations with light damping, aperiodic os-
cillation and aperiodic limit)
•Forced rotary oscillations and their resonance
curves at various degrees of damping
•Phase displacement between the exciter and reso-
nator during resonance
•Chaotic rotary oscillations
•Static determination of the direction variable D
•Dynamic determination of the moment of inertia J
1. Safety instructions
•When removing the torsional pendulum from the
packaging do not touch the scale ring. This could
Torsion Pendulum According to Prof. Pohl 1002956
06/18 ALF
1
2
3
4
5
6
7
8
lead to damage. Always remove using the handles
provided in the internal packaging.
•When carrying the torsional pendulum always hold
it by the base plate.
•Never exceed the maximum permissible supply
voltage for the exciter motor (24 V DC).
•Do not subject the torsional pendulum to any un-
necessary mechanical stress.
2. Description, technical data
The Professor Pohl torsional pendulum consists of a
wooden base plate with an oscillating system and an
electric motor mounted on top. The oscillating system
is a ball-bearing mounted copper wheel (5), which is
connected to the exciter rod via a coil spring (6) that
provides the restoring torque. A DC motor with coarse
and fine speed adjustment is used to excite the tor-
sional pendulum. Excitement is brought about via an
eccentric wheel (14) with connecting rod (13) which
1Exciter motor
2Control knob for fine adjustment of the exciter voltage
3Control knob for coarse adjustment of the exciter voltage
4Scale ring
5Pendulum body
6Coil spring
7Pointer for the exciter phase angle
8Pointer for the pendulum’s phase angle
9Pointer for the pendulum’s deflection
bl Exciter
bm Eddy current brake
bn Guide slot and screw to set the exciter amplitude
bo Connecting rod
bp Eccentric drive wheel
bq 4-mm safety socket for exciter voltage measurement
br 4-mm safety sockets for the exciter motor power supply
bs 4-mm safety sockets for the eddy current brake power
supply
9
bpbobnbmbl
bsbrbq

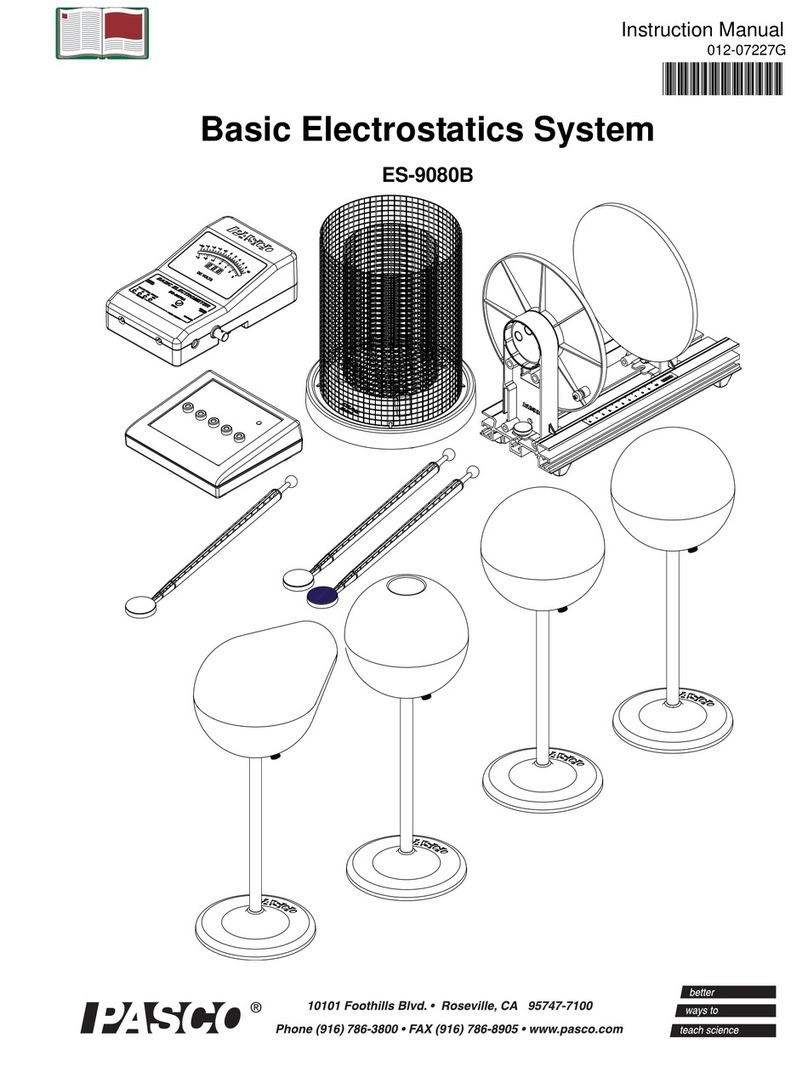
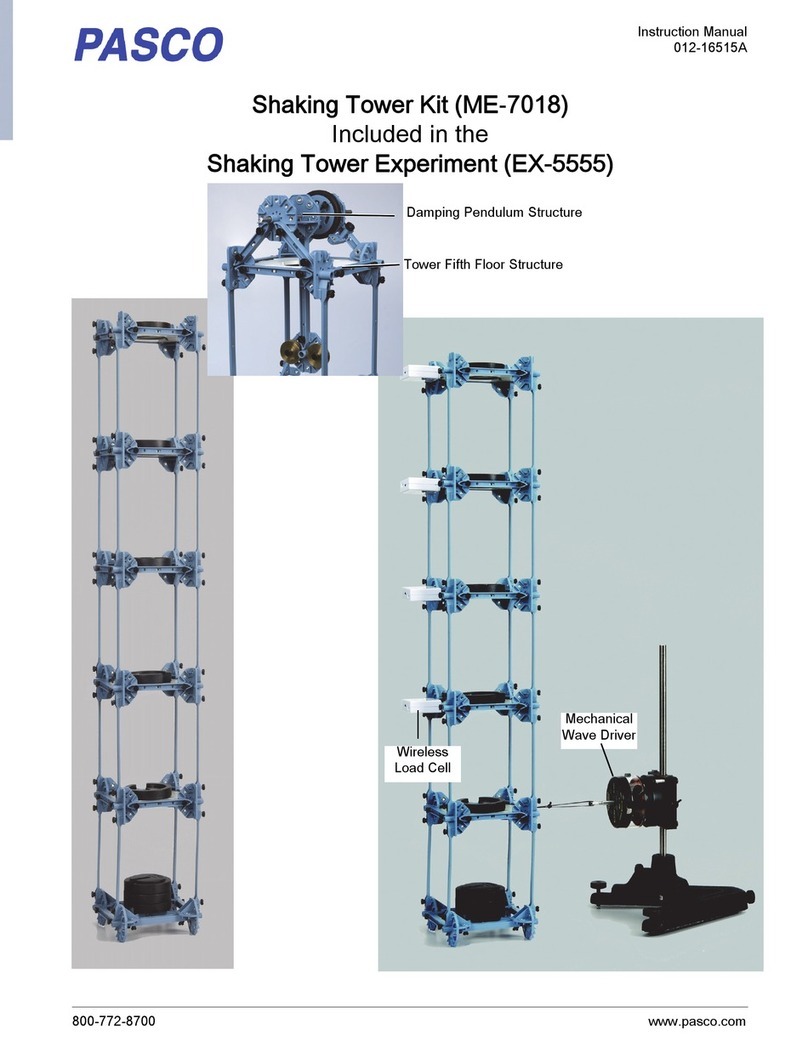
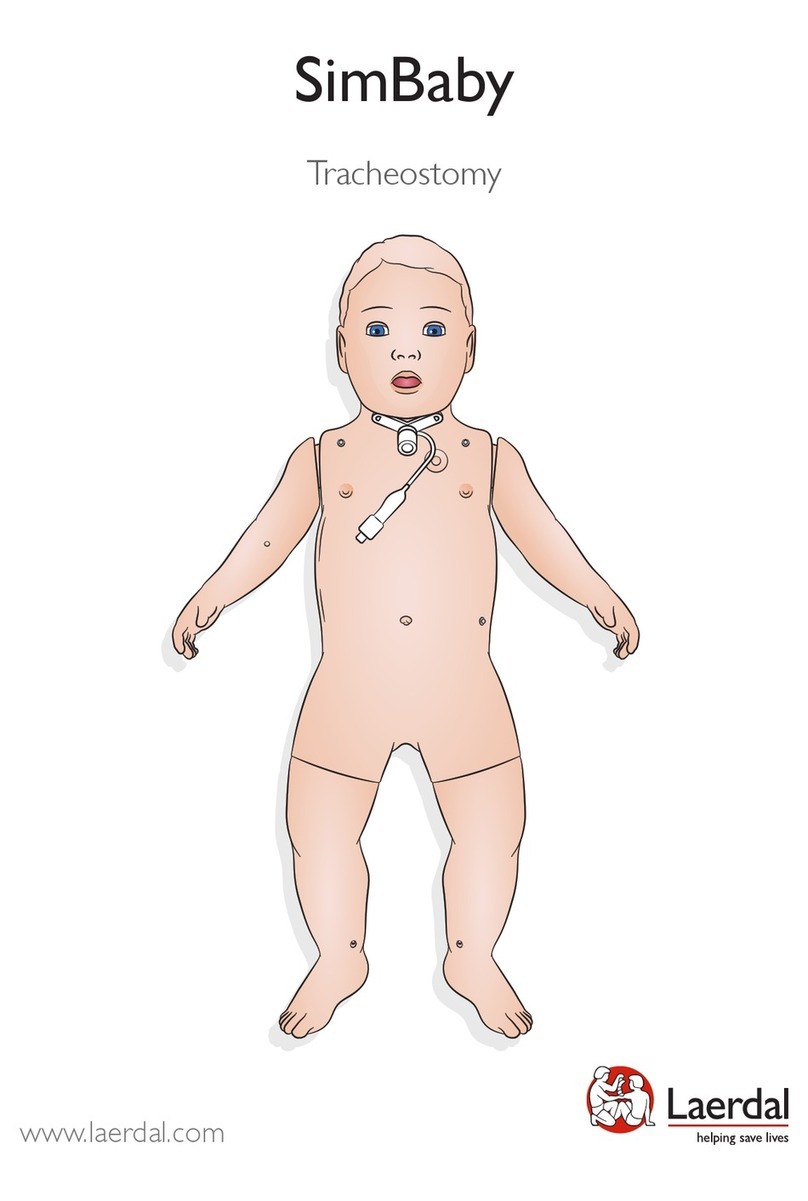
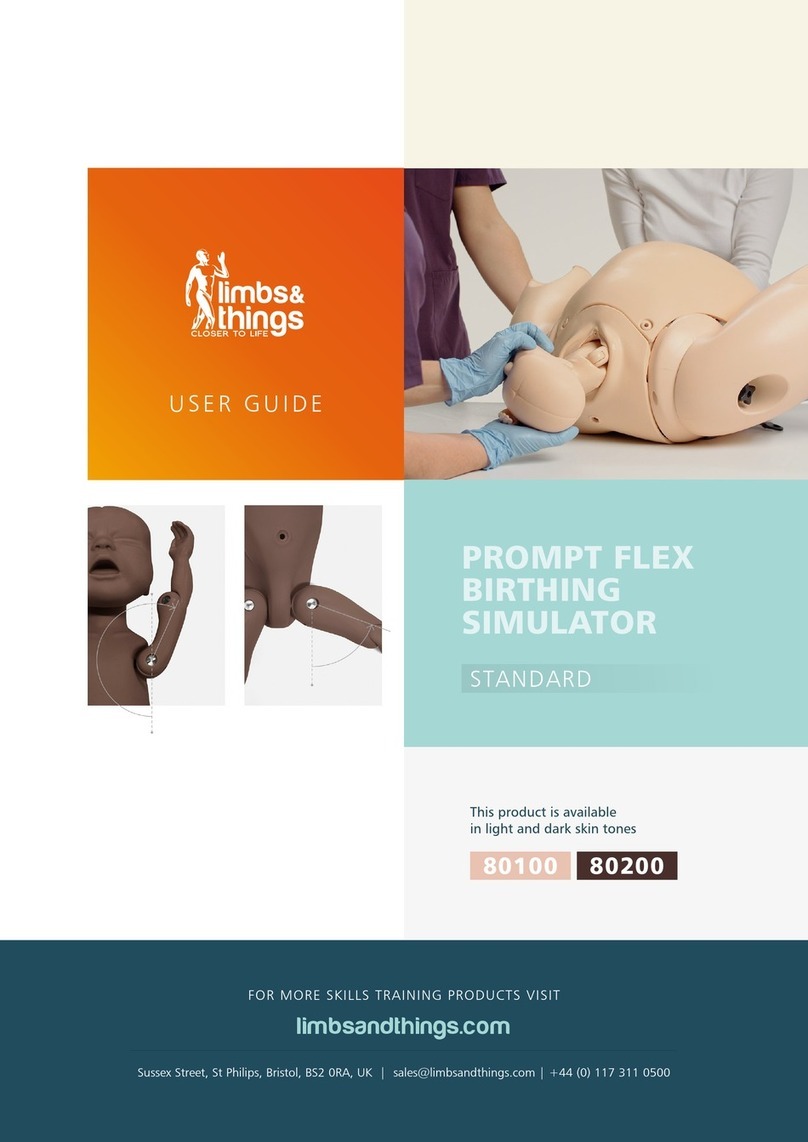
7
unwinds the coil spring then compresses it again in a
periodic sequence and thereby initiates the oscillation
of the copper wheel. The electromagnetic eddy cur-
rent brake (11) is used for damping. A scale ring (4)
with slots and a scale in 2-mm divisions extends over
the outside of the oscillating system; indicators are
located on the exciter and resonator.
The device can also be used in shadow projection dem-
onstrations.
Natural frequency: 0.5 Hz approx.
0 to 1.3 Hz (continuously adjust-Exciter frequency:
able)
Terminals:
Motor: max. 24 V DC, 0.7 A,
via 4-mm safety sockets
Eddy current brake: 0 to 20 V DC, max. 2 A,
via 4-mm safety sockets
Scale ring: 300 mm Ø
400 mm x 140Dimensions: mm x 270 mm
4 kgGround:
2.1 Scope of supply
1 Torsional pendulum
2 Additional 10 g weights
2 Additional 20 g weights
3. Theoretical Fundamentals
3.1 Symbols used in the equations
Angular directional variableD =
Mass moment of inertia=J
Restoring torque=M
Period=T
T0Period of an undamped system=
TdPeriod of the damped system=
M

E
Amplitude of the exciter moment=
Damping torque=b
Frequency=n
Time=t
ΛLogarithmic decrement=
δDamping constant=
ϕ Angle of deflection=
ϕ

0
Amplitude at time t = 0 s=
ϕ

n
Amplitude after n periods=
ϕ

E
Exciter amplitude=
ϕ

S
System amplitude=
ω0Natural frequency of the oscillating system=
ωdNatural frequency of the damped system=
ωEExciter angular frequency=
ωEres Exciter angular frequency for max. amplitude=
Ψ0S System zero phase angle=
3.2 Harmonic rotary oscillation
A harmonic oscillation is produced when the restoring
torque is proportional to the deflection. In the case of
harmonic rotary oscillations the restoring torque is
proportional to the deflection angle ϕ:
M = D · ϕ
The coefficient of proportionality D (angular direction
variable) can be computed by measuring the deflec-
tion angle and the deflection moment.
If the period duration T is measured, the natural reso-
nant frequency of the system ω0is given by
ω
0= 2
π /T
and the mass moment of inertia J is given by
ω
0
2=D
J
3.3 Free damped rotary oscillations
An oscillating system that suffers energy loss due to
friction, without the loss of energy being compensated
for by any additional external source, experiences a
constant drop in amplitude, i.e. the oscillation is
damped.
At the same time the damping torque b is proportional
to the deflectional angle
ϕ
.
.
The following motion equation is obtained for the
torque at equilibrium
JbD⋅+⋅+⋅= ϕϕϕ
.. .0
b = 0 for undamped oscillation.
If the oscillation begins with maximum amplitude
ϕ

0
at t = 0 s the resulting solution to the differential equa-
tion for light damping (δ² < ω0²) (oscillation) is as fol-
lows
ϕ =
ϕ

0
· e–δ·t · cos ( ω
d· t)
δ= b/2 J is the damping constant and
ωωδ
d0
22
=−
the natural frequency of the damped system.
Under heavy damping (δ² > ω0²) the system does not
oscillate but moves directly into a state of rest or equi-
librium (non-oscillating case).
The period duration Tdof the lightly damped oscillat-
ing system varies only slightly from T0of the undamped
oscillating system if the damping is not excessive.
By inserting t= n· Tdinto the equation
ϕ =
ϕ

0
· e–δ·t · cos ( ω
d· t)
and ϕ =
ϕ

n
for the amplitude after n periods we ob-
tain the following with the relationship ω
d= 2
π /Td
ϕ
ϕ
δ


n
0
d
=⋅
−⋅
eT
n
and thus from this the logarithmic decrement Λ:
Λ =⋅ =⋅






=







δϕ
ϕ
ϕ
ϕ
TnInIn
d
n
0
n
n+1
1





8
By inserting δ = Λ /Td, ω
0= 2
π /T0and ω
d= 2
π /Td
into the equation
ωωδ
d0
22
=−
we obtain:
TT
d0
2
2
=⋅+14
Λ
π
whereby the period Tdcan be calculated precisely pro-
vided that T0is known.
3.4 Forced oscillations
In the case of forced oscillations a rotating motion with
sinusoidally varying torque is externally applied to the
system. This exciter torque can be incorporated into
the motion equation as follows:
JbD M t⋅+⋅+⋅= ⋅ ⋅
()
ϕϕϕ ω
.. .sin

EE
After a transient or settling period the torsion pendu-
lum oscillates in a steady state with the same angular
frequency as the exciter, at the same time ωEcan still
be phase displaced with respect to ω0. Ψ0S is the sys-
tem’s zero-phase angle, the phase displacement be-
tween the oscillating system and the exciter.
ϕ =
ϕ

S
· sin ( ω
E· t–
Ψ
0S)
The following holds true for the system amplitude
ϕ

S
ϕ
ωω δω


=
−
()
+⋅
M
J
E
0
2E 22
E
2
4
2
The following holds true for the ratio of system ampli-
tude to the exciter amplitude
ϕ
ϕω
ω
δ
ω
ω
ω



S
E
E
E
0
22
0
2
E
0
2
=
−











+



⋅




M
J
14
In the case of undamped oscillations, theoretically
speaking the amplitude for resonance (ωEequal to ω0)
increases infinitely and can lead to “catastrophic reso-
nance”.
In the case of damped oscillations with light damping
the system amplitude reaches a maximum where the
exciter’s angular frequency ωE res is lower than the sys-
tem’s natural frequency. This frequency is given by
ωω δ
ω
Eres 0
2
0
2
=⋅−12
Stronger damping does not result in excessive ampli-
tude.
For the system’s zero phase angle Ψ0S the following is
true:
Ψ
0S
0
22
=−








arctan 2
δω
ωω
ω
For ωE= ω0(resonance case) the system’s zero-phase
angle is Ψ0S = 90°. This is also true for δ= 0 and the
oscillation passes its limit at this value.
In the case of damped oscillations (δ> 0) where
ωE< ω0, we find that 0° ≤Ψ0S ≤90° and when ωE> ω0
it is found that 90° ≤Ψ0S ≤180°.
In the case of undamped oscillations (δ= 0), Ψ0S = 0°
for ωE< ω0and Ψ0S = 180° for ωE> ω0.
4. Operation
4.1 Free damped rotary oscillations
•Connect the eddy current brake to the variable volt-
age output of the DC power supply for torsion pen-
dulum.
•Connect the ammeter into the circuit.
•Determine the damping constant as a function of
the current.
4.2 Forced oscillations
•Connect the fixed voltage output of the DC power
supply for the torsion pendulum to the sockets (16)
of the exciter motor.
•Connect the voltmeter to the sockets (15) of the
exciter motor.
•Determine the oscillation amplitude as a function
of the exciter frequency and of the supply voltage.
•If needed connect the eddy current brake to the
variable voltage output of the DC power supply for
the torsion pendulum.
4.3 Chaotic oscillations
•To generate chaotic oscillations there are 4 supple-
mentary weights at your disposal which alter the
torsion pendulum’s linear restoring torque.
•To do this screw the supplementary weight to the
body of the pendulum (5).

9
5. Example experiments
5.1 Free damped rotary oscillations
•To determine the logarithmic decrement Λ, the
amplitudes are measured and averaged out over
several runs. To do this the left and right deflec-
tions of the torsional pendulum are read off the
scale in two sequences of measurements.
•The starting point of the pendulum body is located
at +15 or –15 on the scale. Take the readings for
five deflections.
•From the ratio of the amplitudes we obtain Λus-
ing the following equation
Λ =







In
ϕ
ϕ


n
n+1
n
ϕ

–
ϕ

+
0 –15 –15 –15 –15 15 15 15 15
1 –14.8 –14.8 –14.8 –14.8 14.8 14.8 14.8 14.8
2 –14.4 –14.6 –14.4 –14.6 14.4 14.4 14.6 14.4
3 –14.2 –14.4 –14.0 –14.2 14.0 14.2 14.2 14.0
4 –13.8 –14.0 –13.6 –14.0 13.8 13.8 14.0 13.8
5 –13.6 –13.8 –13.4 –13.6 13.4 13.4 13.6 13.6
nØ
ϕ

– Ø
ϕ

+ Λ – Λ +
0 –15 15
1 –14.8 14.8 0.013 0.013
2 –14.5 14.5 0.02 0.02
3 –14.2 14.1 0.021 0.028
4 –13.8 13.8 0.028 0.022
5 –13.6 13.5 0.015 0.022
•The average value for Λcomes to Λ= 0.0202.
•For the pendulum oscillation period T the follow-
ing is true: t = n · T. To measure this, record the
time for 10 oscillations using a stop watch and cal-
culate T.
T= 1.9 s
•From these values the damping constant δcan be
determined from δ= Λ/ T.
δ = 0.0106 s–1
•For the natural frequency ωthe following holds
true
ωπδ =



−
2
T
2
2
ω = 3.307 Hz
5.2 Free damped rotary oscillations
•To determine the damping constant δas a func-
tion of the current Ιflowing through the electro-
magnets the same experiment is conducted with
an eddy current brake connected at currents of
Ι= 0.2 A, 0.4 A and 0.6 A.
ΙΙ
ΙΙ
Ι= 0.2 A
n
ϕ

– Ø
ϕ

– Λ –
0 –15 –15 –15 –15 –15
1 –13.6 –13.8 –13.8 –13.6 –13.7 0.0906
2 –12.6 –12.8 –12.6 –12.4 –12.6 0.13
3 –11.4 –11.8 –11.6 –11.4 –11.5 0.0913
4 –10.4 –10.6 –10.4 –10.4 –10.5 0.0909
5 9.2 –9.6 –9.6 –9.6 –9.5 0.1
•For T = 1.9 s and the average value of Λ= 0.1006
we obtain the damping constant: δ= 0.053 s–1
ΙΙ
ΙΙ
Ι= 0.4 A
n
ϕ

– Ø
ϕ

– Λ –
0 –15 –15 –15 –15 –15
1 –11.8 –11.8 –11.6 –11.6 –11.7 0.248
2 –9.2 –9.0 –9.0 –9.2 –9.1 0.25
3 –7.2 –7.2 –7.0 –7.0 –7.1 0.248
4 –5.8 –5.6 –5.4 –5.2 –5.5 0.25
5 –4.2 –4.2 –4.0 –4.0 –4.1 0.29
•For T = 1.9 s and an average value of Λ= 0.257 we
obtain the damping constant: δ= 0.135 s–1
ΙΙ
ΙΙ
Ι= 0.6 A
n
ϕ

– Ø
ϕ

– Λ –
0 –15 –15 –15 –15 –15
1 –9.2 –9.4 –9.2 –9.2 –9.3 0.478
2 –5.4 –5.2 –5.6 –5.8 –5.5 0.525
3 –3.2 –3.2 –3.2 –3.4 –3.3 0.51
4 –1.6 –1.8 –1.8 –1.8 –1.8 0.606
5 –0.8 –0.8 –0.8 –0.8 –0.8 0.81
•For T = 1.9 s and an average value of Λ= 0.5858
we obtain the damping constant: δ= 0.308 s–1
5.3 Forced rotary oscillation
•Take a reading of the maximum deflection of the
pendulum body to determine the oscillation am-
plitude as a function of the exciter frequency or
the supply voltage.
T = 1.9 s
Motor voltage V
ϕ

3 0.8
4 1.1
5 1.2
6 1.6
7 3.3
7.6 20.0
8 16.8
9 1.6
10 1.1

10
•After measuring the period T the natural frequency
of the system ω0can be obtained from
ω
0= 2 π/T = 3.3069 Hz
•The most extreme deflection arises at a motor volt-
age of 7.6 V, i.e. the resonance case occurs.
•Then the same experiment is performed with an
eddy current brake connected at currents of
Ι= 0.2 A, 0.4 A and 0.6 A.
ΙΙ
ΙΙ
Ι= 0.2 A
Motor voltage V
ϕ

3.0 0.9
4.0 1.1
5.0 1.2
6.0 1.7
7.0 2.9
7.6 15.2
8.0 4.3
9.0 1.8
10.0 1.1
ΙΙ
ΙΙ
Ι= 0.4 A
Motor voltage V
ϕ

3.0 0.9
4.0 1.1
5.0 1.3
6.0 1.8
7.0 3.6
7.6 7.4
8.0 3.6
9.0 1.6
10.0 1.0
ΙΙ
ΙΙ
Ι= 0.6 A
Motor voltage V
ϕ

3.0 0.9
4.0 1.1
5.0 1.2
6.0 1.6
7.0 2.8
7.6.0 3.6
8.0 2.6
9.0 1.3
10.0 1.0
•From these measurements the resonance curves can
be plotted in a graph depicting the amplitudes
against the motor voltage.
•The resonant frequency can be determined by find-
ing the half-width value from the graph.
Resonance curves
1
5
10
15
20
A
[skt]
012 345678910
I=0,0A
I=0,2A
I=0,4A
I=0,6A
u[v]
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com • Technical amendments may occur