4
5. Versuchsbeispiele
5.1 Freie gedämpfte Drehschwingung
•Zur Bestimmung des logarithmischen Dekrements
Λwerden die Amplituden in mehrfachen Durch-
läufen gemessen und gemittelt. Dazu werden in
zwei Messreihen die Ausschläge des Drehpendels
auf der Skala jeweils links und rechts abgelesen.
•Der Startpunkt des Pendelkörpers lag bei 15 bzw.
–15 auf der Skala. Fünf Ausschläge wurden abgele-
sen.
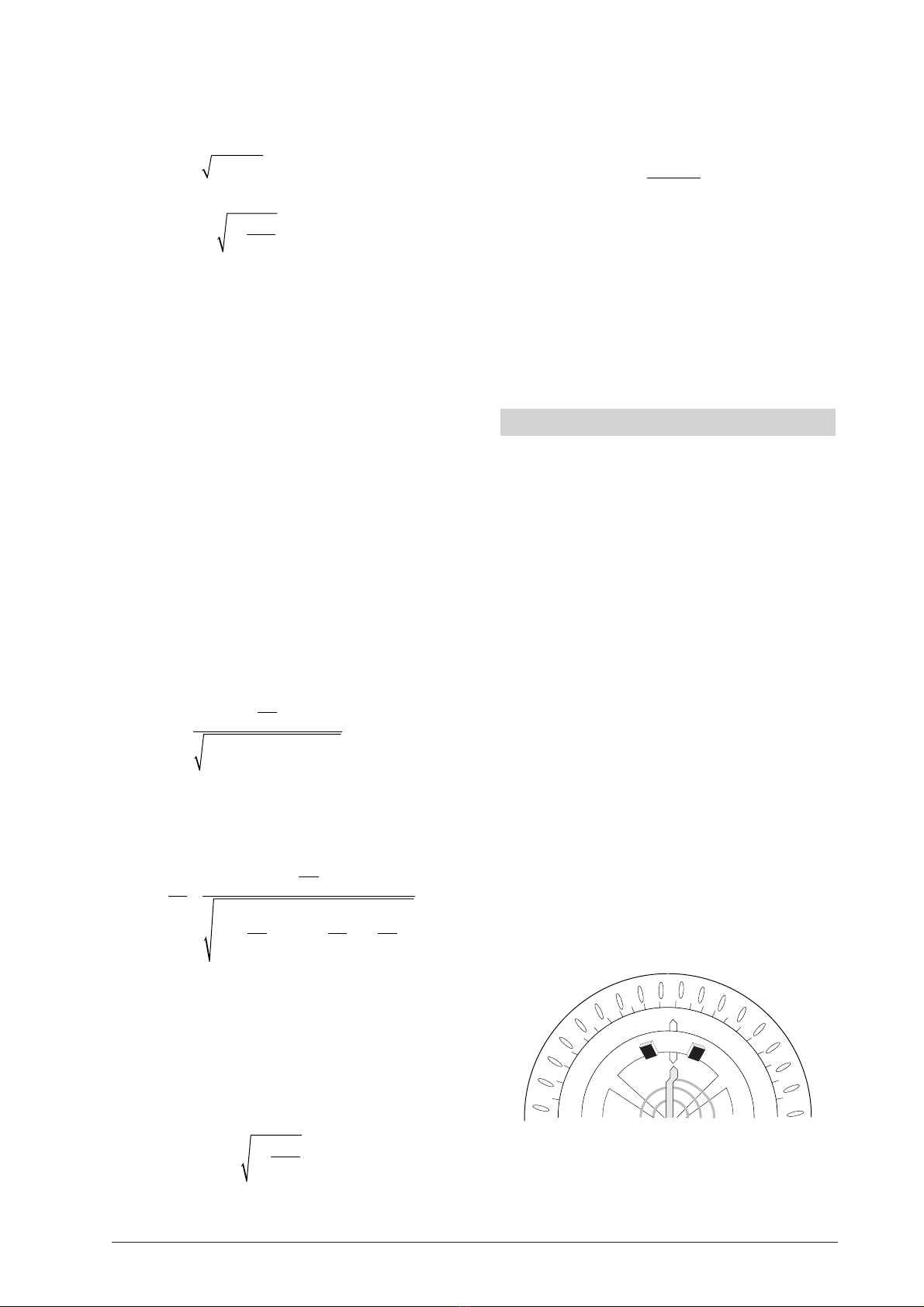
•Aus dem Verhältnis der Amplituden ergibt sich Λ
nach der Formel
Λ
=
In
ϕ
ϕ
n
n+1
n
ϕ
–
ϕ
+
0 –15 –15 –15 –15 15 15 15 15
1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8
2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4
3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0
4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8
5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6
nØ
ϕ
– Ø
ϕ
+
Λ
–
Λ
+
0 –15 15
1 –14,8 14,8 0,013 0,013
2 –14,5 14,5 0,02 0,02
3 –14,2 14,1 0,021 0,028
4 –13,8 13,8 0,028 0,022
5 –13,6 13,5 0,015 0,022
•Der gemittelte Wert für Λbeträgt Λ= 0,0202.
•Für die Schwingungsdauer T des Pendels gilt
t = n · T. Dazu die Zeit für 10 Schwingungen mit
einer Stoppuhr messen und T berechnen.
T= 1,9 s
•Aus diesen Werten lässt sich die Dämpfungs-
konstante δmit δ= Λ/ T bestimmen.
δ
= 0,0106 s–1
•Für die Eigenfrequenz ωgilt
ωπδ
=
−
2
T
2
2
ω
= 3,307 Hz
5.2 Freie gedämpfte Drehschwingung
•Zur Bestimmung der Dämpfungskonstante δin Ab-
hängigkeit vom Strom Ιdurch den Elektromagne-
ten wurde der gleiche Versuch mit zugeschalteter
Wirbelstrombremse bei Ι= 0,2 A, 0,4 A und 0,6 A
durchgeführt.
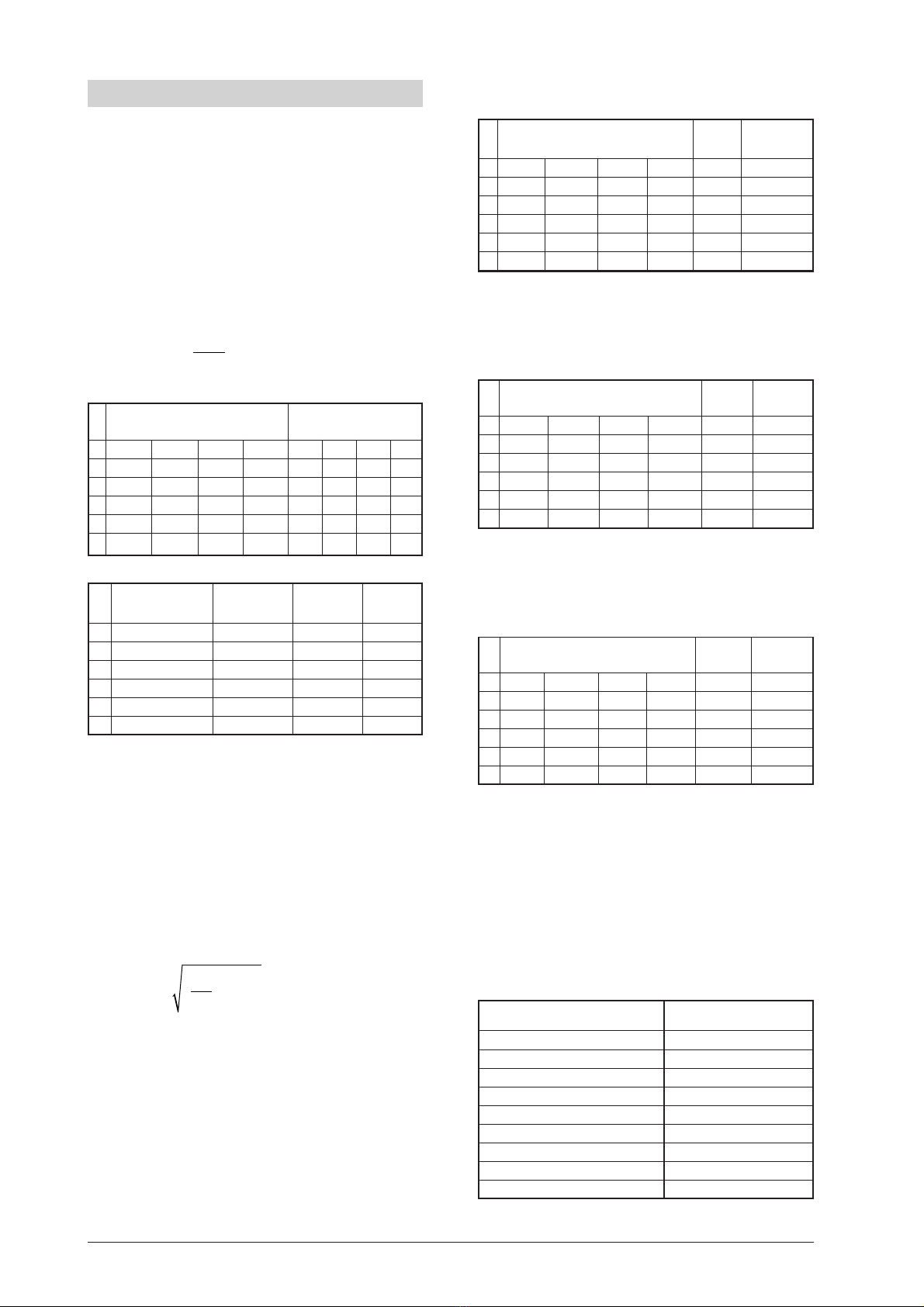
ΙΙ
ΙΙ
Ι= 0,2 A
n
ϕ
– Ø
ϕ
– Λ –
0 –15 –15 –15 –15 –15
1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906
2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13
3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913
4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909
5 9,2 –9,6 –9,6 –9,6 –9,5 0,1
•Bei T = 1,9 s und gemitteltem Λ= 0,1006 ergibt
sich die Dämpfungskonstante: δ= 0,053 s–1
ΙΙ
ΙΙ
Ι= 0,4 A
n
ϕ
– Ø
ϕ
– Λ –
0 –15 –15 –15 –15 –15
1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248
2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25
3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248
4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25
5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29
•Bei T = 1,9 s und gemitteltem Λ= 0,257 ergibt sich
die Dämpfungskonstante: δ= 0,135 s–1
ΙΙ
ΙΙ
Ι= 0,6 A
n
ϕ
– Ø
ϕ
– Λ –
0 –15 –15 –15 –15 –15
1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478
2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525
3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51
4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606
5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81
•Bei T = 1,9 s und gemitteltem Λ= 0,5858 ergibt
sich die Dämpfungskonstante: δ= 0,308 s–1
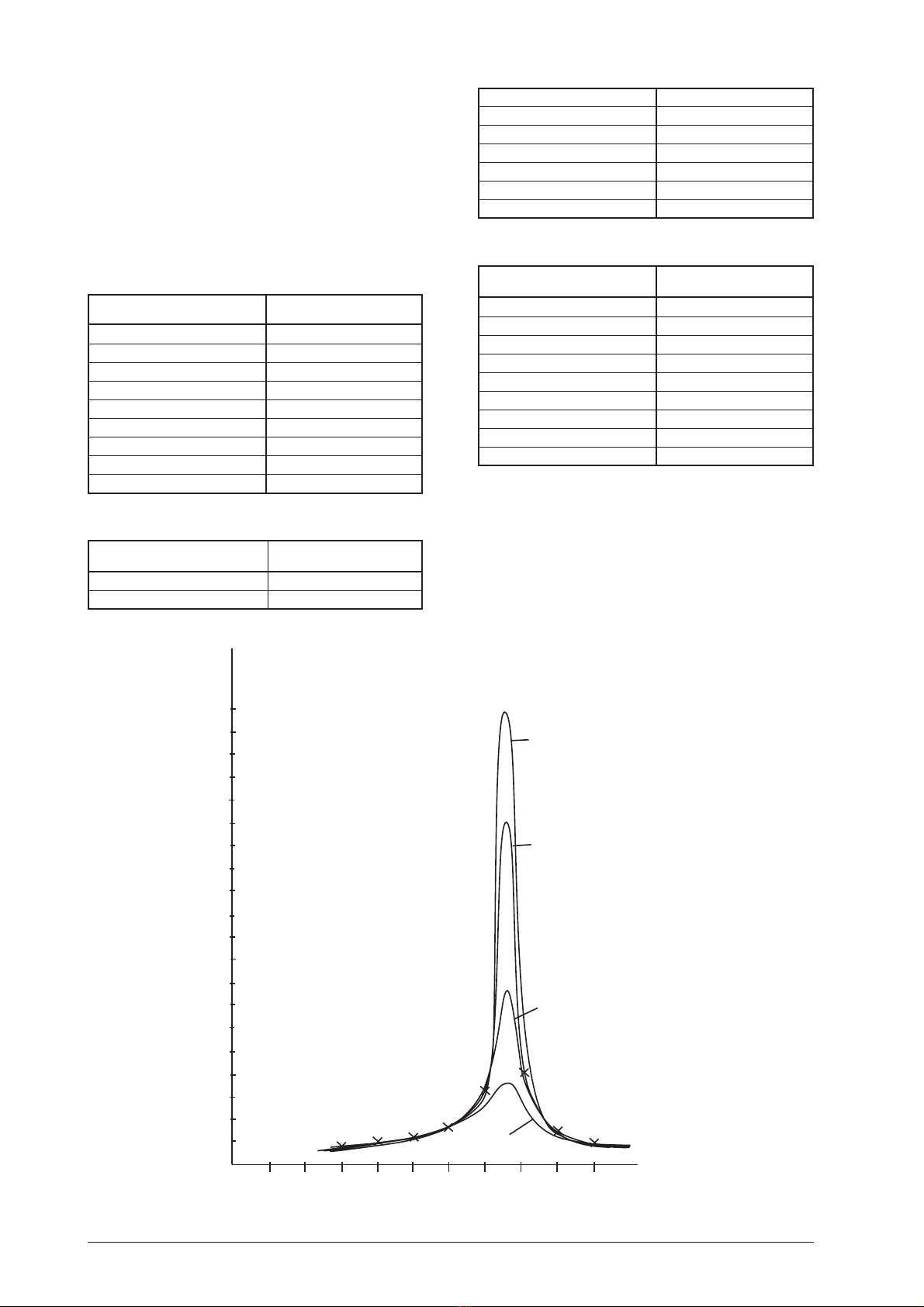
5.3 Erzwungene Drehschwingung
•Zur Bestimmung der Schwingungsamplitude in Ab-
hängigkeit der Erregerfrequenz bzw. der Ver-
sorgungsspannung wird der maximale Ausschlag
des Pendelkörpers abgelesen.
T = 1,9 s
Motorspannung V
ϕ
3 0,8
4 1,1
5 1,2
6 1,6
7 3,3
7,6 20,0
8 16,8
9 1,6
10 1,1