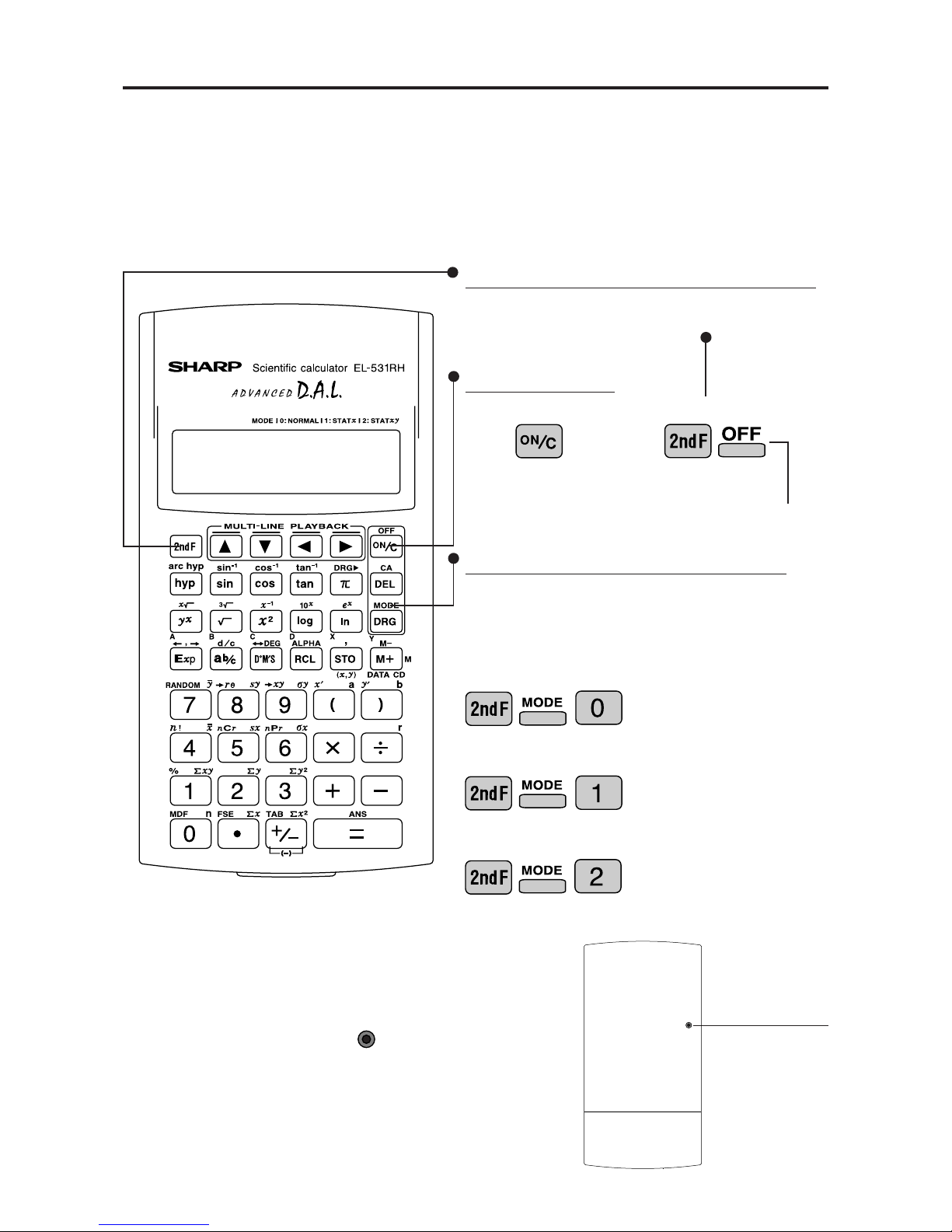
Sharp EL-531RH User manual
Other Sharp Calculator manuals

Sharp
Sharp EL-9900 User manual

Sharp
Sharp SHA2850 - CS-2850H 12-Digit Desktop Display... User manual

Sharp
Sharp ELSI MATE EL-320W User manual

Sharp
Sharp ELSIMATE EL-771C User manual

Sharp
Sharp EL-500W User manual

Sharp
Sharp CS-22C User manual

Sharp
Sharp EL-2902C User manual

Sharp
Sharp EL-546VA User manual

Sharp
Sharp EL-R277B-BK Use and maintenance manual

Sharp
Sharp EL 2196BL - Heavy Duty Color Printing... User manual

Sharp
Sharp EL-1197P User manual

Sharp
Sharp Elsi Mate EL-W211G User manual

Sharp
Sharp ELSI MATE EL-250S User manual

Sharp
Sharp CS-2635RH Installation manual

Sharp
Sharp Elsimate EL-334F User manual

Sharp
Sharp COMPET ELSI-811 User manual

Sharp
Sharp EL-2607RIII User manual

Sharp
Sharp Elsi Mate EK-244T User manual

Sharp
Sharp ELSI MATE EL-326S User manual

Sharp
Sharp ELSI MATE EL-320W User manual