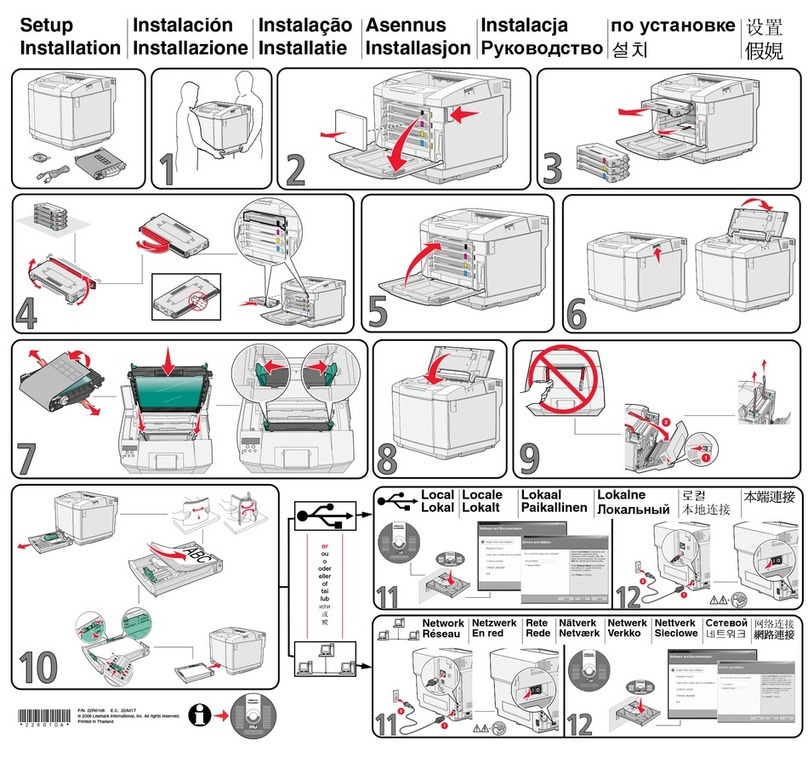
Sindoh D310 Series User manual

ILWIS Applications Guide 131
CHAPTER 11
Determination of peak runoff rate
By:
J.A.M. de Brouwer
Department of Earth Resources Surveys,
International Institute for Aerospace Survey and Earth Sciences (ITC),
P.O. Box 6, 7500 AA Enschede, The Netherlands.
Tel: [phone], Fax: [phone], e-mail: [email protected]
Summary Determine the peak runoff rate of a small watershed using the Modified Rational
Formula method, and the SCS Dimensionless Unit Hydrograph for an excess
rainfall of 1 cm.
Getting startedThe data for this case study are stored on the ILWIS 2.1 CD-ROM in the directory
d:\appguide\chap11. If you have already installed the data on your hard-disk, you
should start up ILWIS and change to the subdirectory where the data files for this
chapter are stored, c:\ilwis21\data\appguide\chap11. If you did not install the
data for this case study yet, please run the ILWIS installation program (see ILWIS
Installation Guide).
F
• Double-click the ILWIS program icon in the ILWIS program group.
• Change the working drive and the working directory until you are in
the directory c:\ilwis21\data\appguide\chap11.
Now you are ready to start the exercises of this case study.

Determination of peak runoff rate
132 ILWIS Applications Guide
11.1 Determination of peak runoff rate using the Modified
Rational Formula
One important empirical formula for determining the peak rate of runoff is the
Rational Formula. This approach was introduced more than 100 years ago. Since
then it has become the most widely used method for designing drainage facilities
for small urban and rural watersheds. It is characterized by (1) consideration of the
entire drainage area as a single unit, (2) estimation of flow at only the most
downstream point, and (3) the assumption that rainfall is uniformly distributed over
the drainage area.
The rational method is described by the formula 11.1.
p
Q
=0.28 CIA
∗ ∗ ∗
[11.1]
where,
Qp= Peak runoff rate [m3/sec].
C = Runoff coefficient.
I = Rainfall intensity [mm/hr].
A = Drainage area [km2].
In the modified version of the rational formula, a storage coefficient, Cs, is included
to account for a recession time > the time the hydrograph takes to rise. In the
original formula the recession time was assumed to be equal to the time of rise.
The modified rational method is then described by the formula 11.2.
ps
Q=0.28 CxC IA
∗ ∗ ∗
[11.2]
The rational method follows the assumptions that (1) the predicted peak discharge
has the same probability of occurrence (return period) as the used rainfall intensity
and (2) the runoff coefficient is constant during the rain storm.
A rainfall with a steady uniform intensity applied to the catchment will cause
runoff that will reach its maximum rate when all parts of the watershed are
contributing to the outflow. This will happen after the elapsed time tc, the time of
concentration. At this time the runoff rate equals the excess rainfall rate.
There are a few well defined criteria for selection of formulas or methods for
determining the time of concentration. Therefore the suggestion to (1) check in the
literature the origin (region, climate, etc.) and the watershed scale from which the
formula was derived, and (2) test more than one formula and critically evaluate the
possible differences.
A number of formulas and methods for determining tcexist. Only one of them will
be presented here:
Kirpich (Ramser) time of concentration equation. Formula 11.3
c0.77 -0.385
t=0.0195 LS
∗ ∗ (Kirpich/Ramser)[11.3]
where,

Determination of peak runoff rate
ILWIS Applications Guide 133
tc= Time of concentration [min].
L = Length of main river [m].
S = Distance weighted channel slope [m/m].
Available data The materials used in this exercise are:
− Contour and drainage map of the catchment.
− Land use map.
− Soil map with soil attribute table.
− Two tables (Table 11.1 and Table 11.2) with typical C coefficients. Reference
is made to the hydrology text books (Schwab et al., 1993).
Table 11.1: Runoff coefficient C for agricultural watersheds (Soil group B)
Coefficient C for rainfall rates of
Crop and hydrologic condition 25 mm/h 100 mm/h 200 mm/h
Row crop, poor practice 0.63 0.65 0.66
Row crop, good practice 0.47 0.56 0.62
Small grain, poor practice 0.38 0.38 0.38
Small grain, good practice 0.18 0.21 0.22
Meadow, rotation, good 0.29 0.36 0.39
Pasture, permanent, good 0.02 0.17 0.23
Woodland, mature, good 0.02 0.10 0.15
Table 11.2: Hydrologic soil group conversion factors
Factors for converting the runoff coefficient C
from Group B soils to
Crop and hydrologic condition Group A Group C Group D
Row crop, poor practice 0.89 1.09 1.12
Row crop, good practice 0.86 1.09 1.14
Small grain, poor practice 0.86 1.11 1.16
Small grain, good practice 0.84 1.11 1.16
Meadow, rotation, good 0.81 1.13 1.18
Pasture, permanent, good 0.64 1.21 1.31
Woodland, mature, good 0.45 1.27 1.40
Determine time of concentration
In order to determine the time of concentration, the catchment area, for which the
peak runoff rate is going to be determined, has to be inspected on size, land cover
and topography.
F
• Study the catchment area and determine the size of the total
catchment area.
• Study the topography of the catchment area and determine the limits

Determination of peak runoff rate
134 ILWIS Applications Guide
of the slopes to be encountered.
• Study the land use map.
• Calculate the time of concentration using the formula of
Kirpich/Ramser.
Determine the area weighted runoff coefficient
The rational formula uses C, the runoff coefficient. This coefficient is related to the
different land covers and hydrologic soil groups. Within the catchment, more than
one land cover type and soil group exist. In order to find a representative runoff
coefficient, an overall catchment runoff coefficient has to be determined using the
areas of the different land cover/hydrologic soil group complexes as weighing
factor.
F
• Reclassify the soils map into a map showing the Hydrologic Soil
Groups.
• Determine the Land cover/Hydrologic soils group complexes and
determine the areas occupied by the different complexes.
• Calculate the different areas for the different land cover/ Hydrologic
soil group complexes.
• Determine a runoff coefficient for each complex assuming a rainfall
rate of 100 mm/h.
• Calculate the overall catchment runoff coefficient.
Determine the 10-year return period peak runoff rate
When determining the peak runoff rate according to the rational formula a rainfall
intensity, with a certain return period, has to be selected. The duration of the storm
has to equal the time of the concentration of the catchment. In this exercise a
rainfall intensity of 100 mm/h with a return period of 10 years is used.
F
• Calculate the 10-year return period peak runoff rate, assuming a
storage coefficient Csof 0.75.

Determination of peak runoff rate
ILWIS Applications Guide 135
11.2 Determination of peak runoff rate using the SCS
Dimensionless Unit Hydrograph
One important empirical formula for determining the quantity of runoff is the SCS
Dimensionless Unit Hydrograph (U.S. Soil Conservation Service, 1964). It belongs
to the group of isochronal methods for determining peak runoff rates. The method
is based on the theory of Sherman (1932). The analysis of a large number of unit
hydrographs from catchments of a wide range in size and from different locations
led to the formulation of the SCS dimensionless unit hydrograph. In order to use
this method the time to peak tpeak and the peak discharge qpeak are estimated. The
method assumes that (1) the duration of excess rainfall, D, is less or equal to 0.133
x the time of concentration tcand (2) the rainfall duration is not too long (D<0.2
tpeak ). If these conditions are met the formulas 11.4, 11.5 and 11.6 can be used.
peak lag
t=D
2
+t[11.4]
where,
tpeak = Time to peak [hr].
D = Duration of excess rainfall [hr].
tlag = The lag time of the watershed [hr].
and,
lag c
t=0.6 t[11.5]
where,
tc= Time of concentration [hr].
The peak runoff rate can be calculated using the formula 11.6.
peak peak
q=2.08 RO A
t[11.6]
where,
qpeak = Peak runoff rate [m3/s].
RO = Storm runoff or excess rainfall volume [cm].
A = Watershed area [km2].
tpeak = Time to peak [hr].
The lag time can be calculated using formula 11.7, proposed by the SCS for
estimating lag times of runoff for agricultural, forest and range lands watersheds.

Determination of peak runoff rate
136 ILWIS Applications Guide
lag
0.8 0.7
0.5
t=2.587 L1000
CN -9
1900
H
∗




∗[11.7]
where,
tlag = Lag time [hr].
L = Hydraulic watershed length [m].
CN = Hydrologic area-weighted curve number.
H = Average watershed land slope [%].
The hydraulic watershed length L can be approximated for small watersheds
(<2000 ha) by the formula 11.8.
L =110
A
0.6 [11.8]
where,
A = watershed area [ha].
The curve numbers CN can be derived from tables that provide SCS Curve
Numbers for various soils/land cover complexes. The Curve Numbers can be
adjusted by correcting them for antecedent moisture conditions. For the curve
number tables, reference is made to the hydrology text books.
Available data The materials used in this exercise are:
− Land use map.
− Soil map with soil attribute table.
− A table (Table 11.3) with typical curve numbers. Reference is made to the
hydrology text books (Schwab et al., 1993).
Table 11.3: Runoff curve number for hydrologic soil-cover complexes for antecedent rainfall
condition II and Ia=2S Hydrologic soil group
Land use or crop Treatment or
practice Hydrologic condition AB C D
Fallow Straight row -77 86 91 94
Row crops Straight row Poor 72 81 88 91
Straight row Good 67 78 85 89
Contoured Poor 70 79 84 88
Contoured Good 65 75 82 86
Terraced Poor 66 74 80 82
Terraced Good 62 71 78 81
Small grain Straight row Poor 65 76 84 88
Straight row Good 63 75 83 87
Contoured Poor 63 74 82 85
Contoured Good 61 73 81 84
Terraced Poor 61 72 79 82

Determination of peak runoff rate
ILWIS Applications Guide 137
Table 11.3: Runoff curve number for hydrologic soil-cover complexes for antecedent rainfall
condition II and Ia=2S (Cont.) Hydrologic soil group
Land use or crop Treatment or
practice Hydrologic condition AB C D
Terraced Good 59 70 78 81
Close-seeded legumes Straight row Poor 66 77 85 89
or rotation meadow Straight row Good 58 72 81 85
Contoured Poor 64 75 83 85
Contoured Good 55 69 78 83
Terraced Poor 63 73 80 83
Terraced Good 51 67 76 80
Pasture or range Poor 68 79 86 89
Fair 49 69 79 84
Good 39 61 74 80
Contoured Poor 47 67 81 88
Meadow (permanent) Good 30 58 71 78
Woods (farm woodlots) Poor 45 66 77 83
Fair 36 60 73 79
Good 25 55 70 77
Farmsteads -59 74 82 86
Roads and right-of-way
(hard surface) -74 84 90 92
Determine the area-weighed curve number
The SCS method uses curve numbers. These numbers are related to the different
land cover types, soil properties and the antecedent moisture. Within the catchment
more than one land cover type and soil type exist. In order to find a representative
curve number, an overall catchment curve number has to be determined using the
areas of the different land cover and soil types as weighing factor.
F
• Study the catchment area and determine the size of the total
catchment area.
• Reclassify the soils map into a map showing the Hydrologic Soil
Groups.
• Determine the Hydrologic soils group/Land cover complexes and
determine the areas occupied by the different complexes.
• Select for each Hydrologic soils group/Land cover complex a curve
number assuming antecedent rainfall condition II and Ia=0.2S.
• Calculate the overall catchment curve number.
Determine the lag time
For the calculation of the lag time a number of watershed parameters have to be
determined.

Determination of peak runoff rate
138 ILWIS Applications Guide
F
• Calculate the Hydraulic watershed length.
• Determine the average watershed land slope.
• Calculate the lag time tlag.
Determine the unit duration of excess rainfall
The application of the SCS dimensionless unit hydrograph is only valid for storms
with a duration less than 0.133 x time of concentration.
F
• Calculate the duration D of excess rainfall using
D=0.133*Tc.
Determine the peak runoff rate for 1 cm of excess rainfall
When calculating the peak runoff of any unit hydrograph the amount of excess
rainfall equals a unit depth, i.e. 1 mm or 1 cm. Based on the unit hydrograph the
peak flow rate for other storms with a different rainfall excess amount can be
calculated.
F
• Calculate the peak runoff rate for a total amount of excess rainfall of
1 cm.
References
Schwab, G.O., Fangmeier, D.D., Elliot, W.J. and Freveret, R.K. (1993). Soil and
water conservation engineering. J. Wiley and sons. New York. 507 pp.
Sherman, L.K. (1932). Stream-flow from rainfall by the unit-graph method. Eng.
News-Rec. 108: 501-505.
U.S. Soil Conservation Service. (1964). Hydrology. Section 4, SCS National
Engineering Handbook. Washington, D.C.