1. Colour, and the effects of colour filters
Observe the colours of the LEDs, the
sequence corresponds to a rainbow or
spectrum produced by a prism.
Work in a dark corner, look at the LED
array through a variety of colour filters.
When a red filter is used, the red LEDs
appear brighter than the rest. The red
filter allows red light to pass and blocks
other colours.
When a green filter is used, the green
LEDs appear brighter than the rest. Green
light passes through, and other colours
are blocked.
You can see more than one colour of LED,
through any particular filter.
Filter materials allow a small range of
colours to pass, so the green filter might
allow green, plus some blue and yellow
light to pass.
If you have two filters of the same colour,
use them to make a “double filter” and
look at the LED array again. You should
find that the blocking of other colours is
more effective.
No matter which filter you use, the white
LED looks the colour of the filter. This is
because the white LED (like any source of
white light) contains all colours.
2. Effect of a diffraction grating, and the
link to colour and wavelength
A diffraction grating is a set of very fine,
parallel lines ruled very close together on
a transparent film. There may be 50, 300
or even 600 lines per millimetre. You can
check using a microscope.
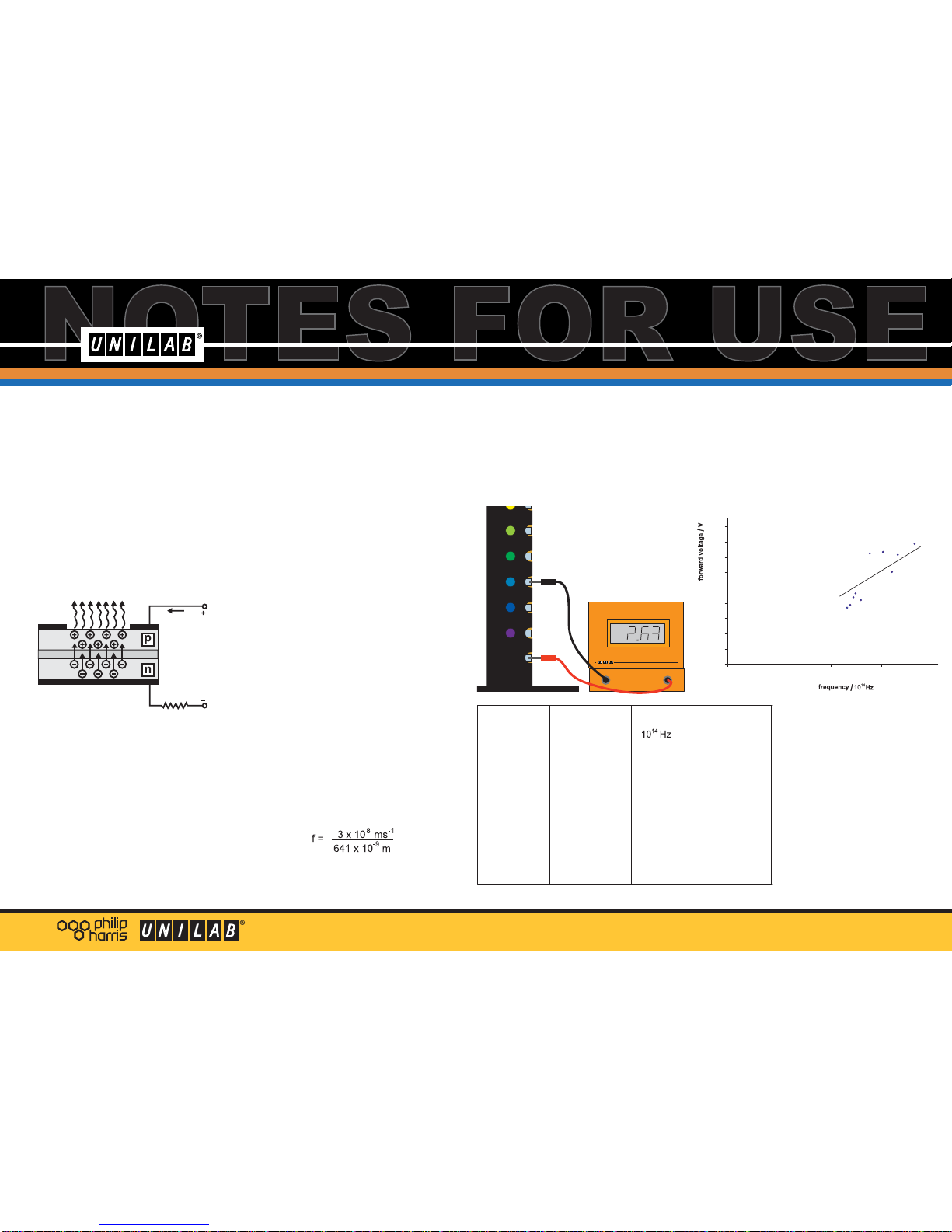
Switch on the LED array.
Hold the grating only by its card frame, to
avoid touching the film.
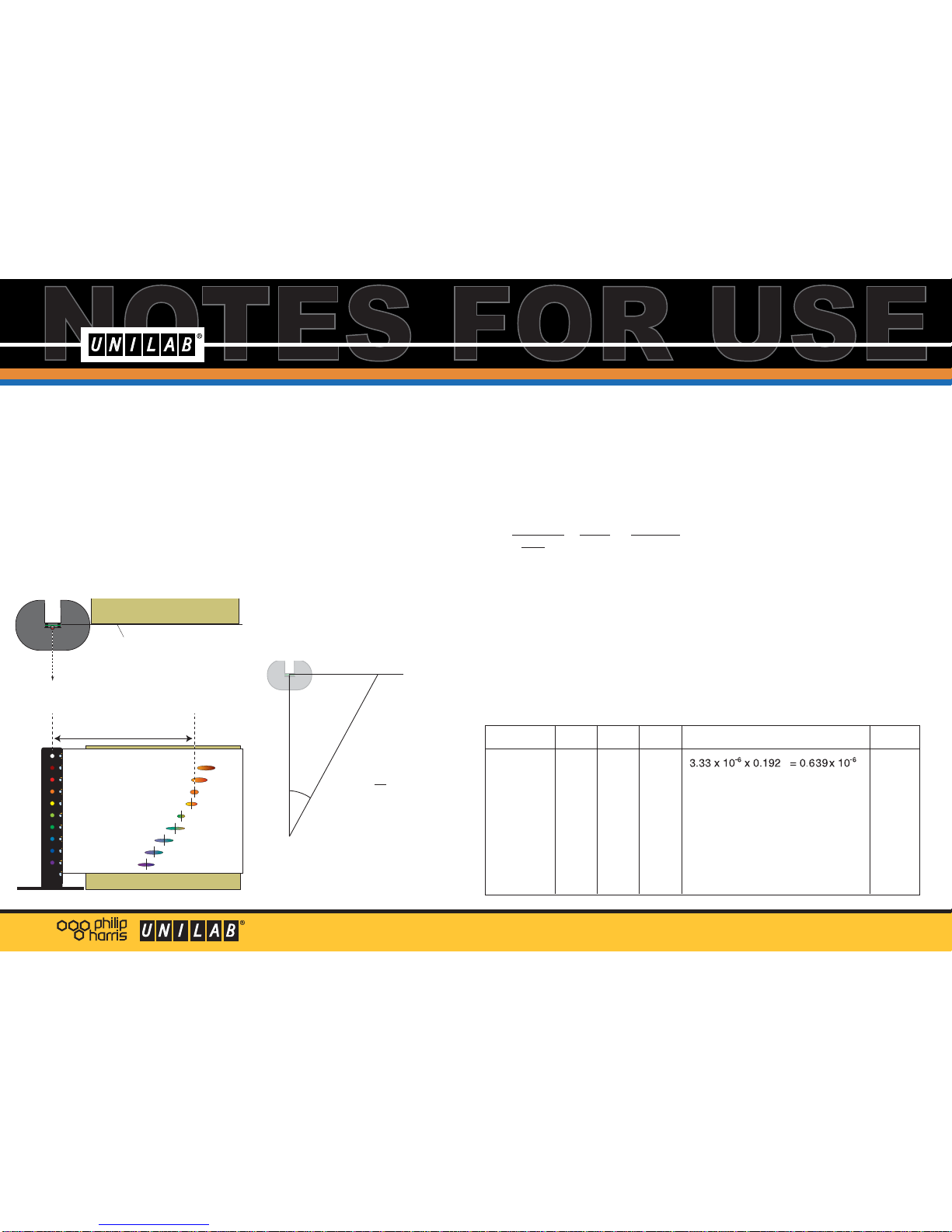
With the grating close to one eye, look at
the LED array. Sketch what you see.
What happens to the light from the white
(top) LED? If you are not sure, ask
someone to cover and uncover the white
LED as you look through the grating.
How does the grating affect red light,
compared with violet light?
You should see the original LEDs, in a
vertical line, with images of the LEDs to
the left and right of the central line.
The white LED gives a spectrum from red
to violet on the left, and violet to red on
the right. Clearly, different colours behave
slightly differently at a diffraction grating.
Colours are separated into a spectrum.
Each LED gives a slightly stretched image,
and not in a single colour! This tells us
that each LED emits a range of colours,
rather than a single colour.
Each LED’s image is also a different
distance from the central line.
Look at the sketch and imagine a number
of single waves, stretching from the
vertical centre line to the image of each
LED. The wave for the red LED is longer
than for the yellow or blue or violet LED.
The lengths of these imaginary waves are
proportional to the actual wavelengths of
the light. What is the approximate
difference between the wavelengths of red
light and violet light?
3. Prediction from initial observations, of
the effect of using a different grating.
You have seen the effect of a diffraction
grating on light of different colours, i.e
light of different wavelengths.
Diffraction is caused by interaction
between light waves and the small gaps
between the lines on the grating.
If we use a grating with more or less lines
per millimetre, how will the image change?
Predict what you expect to see, then test
your prediction using a different grating.
If a ripple tank is available, study the
interaction between plane waves and a
barrier with two gaps in it.
Waves passing through the gaps produce
a diffraction pattern. Here is a typical
pattern, showing first order diffraction (F).
Change the wavelength or the size and
separation of the gaps in the barrier.
Observe changes in the diffraction pattern.