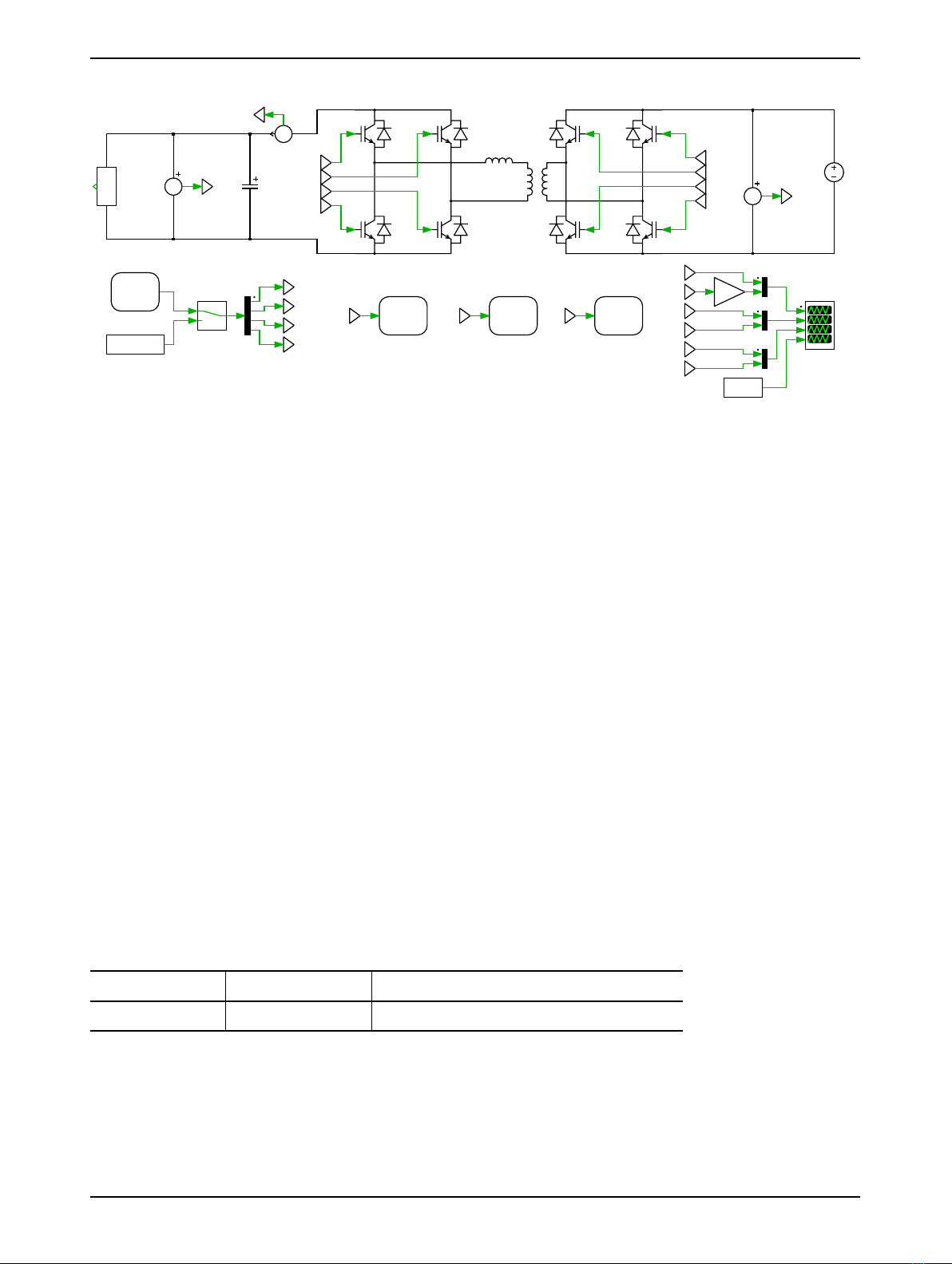
Dual Active Bridge Converter
PWM generation
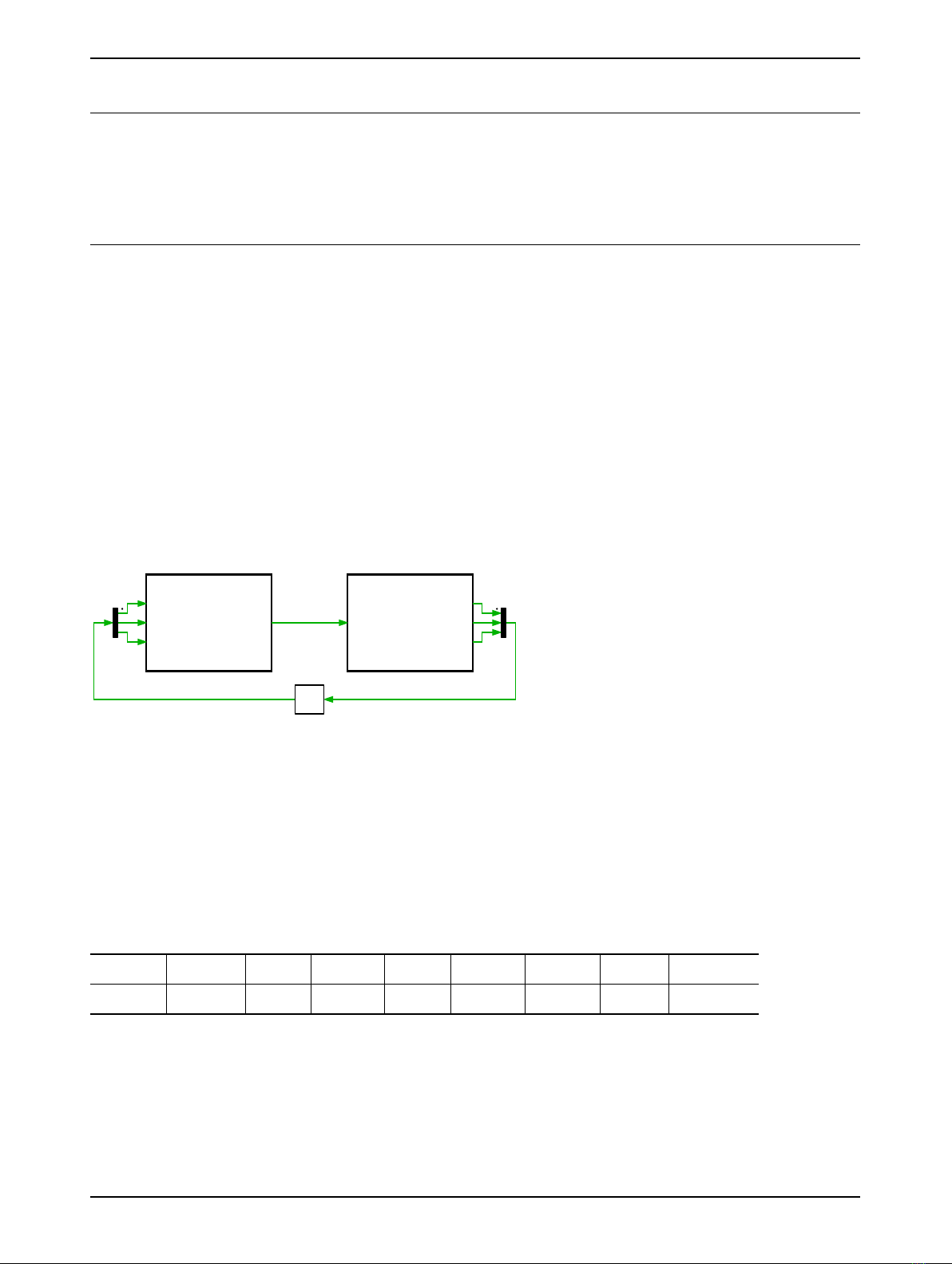
The control calculates the phase shift angle that needs to be applied to the FBs to regulate the cur-
rent. A PWM Out (Variable) block from the RT Box Target Support Library is used, since it allows the
phase shift between the PWM carriers to be dynamically adjusted. The block accepts carrier phase
shift values for each PWM channel from 0 to 1 in p.u. (i.e. 0 means 0◦phase shift and 1 means 360◦
phase shift). The first channel defined in the PWM block acts as master, therefore, the phase shift
specified for the rest of the channels sets the phase shift with respect to the master channel. It is im-
portant to remark that the block does not accept negative phase shift values.
In order to adapt the phase shift angle from radians to p.u. and account for negative values, the fol-
lowing implementation is provided in this demo model:
Φp.u.= sign(Φrad) + 1
2π·Φrad sign(Φrad) =
0,if Φrad ≥0
1,if Φrad <0
(3)
For the DAB implementation four different PWM signals need to be generated, two for each FB. The
two PWM signals for the same FB are phase-shifted 180◦. An additional phase shift is applied to the
PWM signals of the HV FB with respect the PWM signals of the LV FB. In total 4 phase shift angles
need to be provided.
For implementations where the sampling and switching periods are equal, the phase shift provided
for the first (master) PWM channel is commonly set to zero. However, with oversampling, the first
PWM has to be shifted. The reason for this is the following: the counters configured with the “PWM
Out (Variable)” block, are restarted every time the blocks are executed, every Tdisc.Acq in this particu-
lar case. Since Tdisc.Acq is significantly smaller than the switching period, Tdisc.Control, the PWM output
signal are not generated properly. In order to account for this behavior, the master PWM is shifted. A
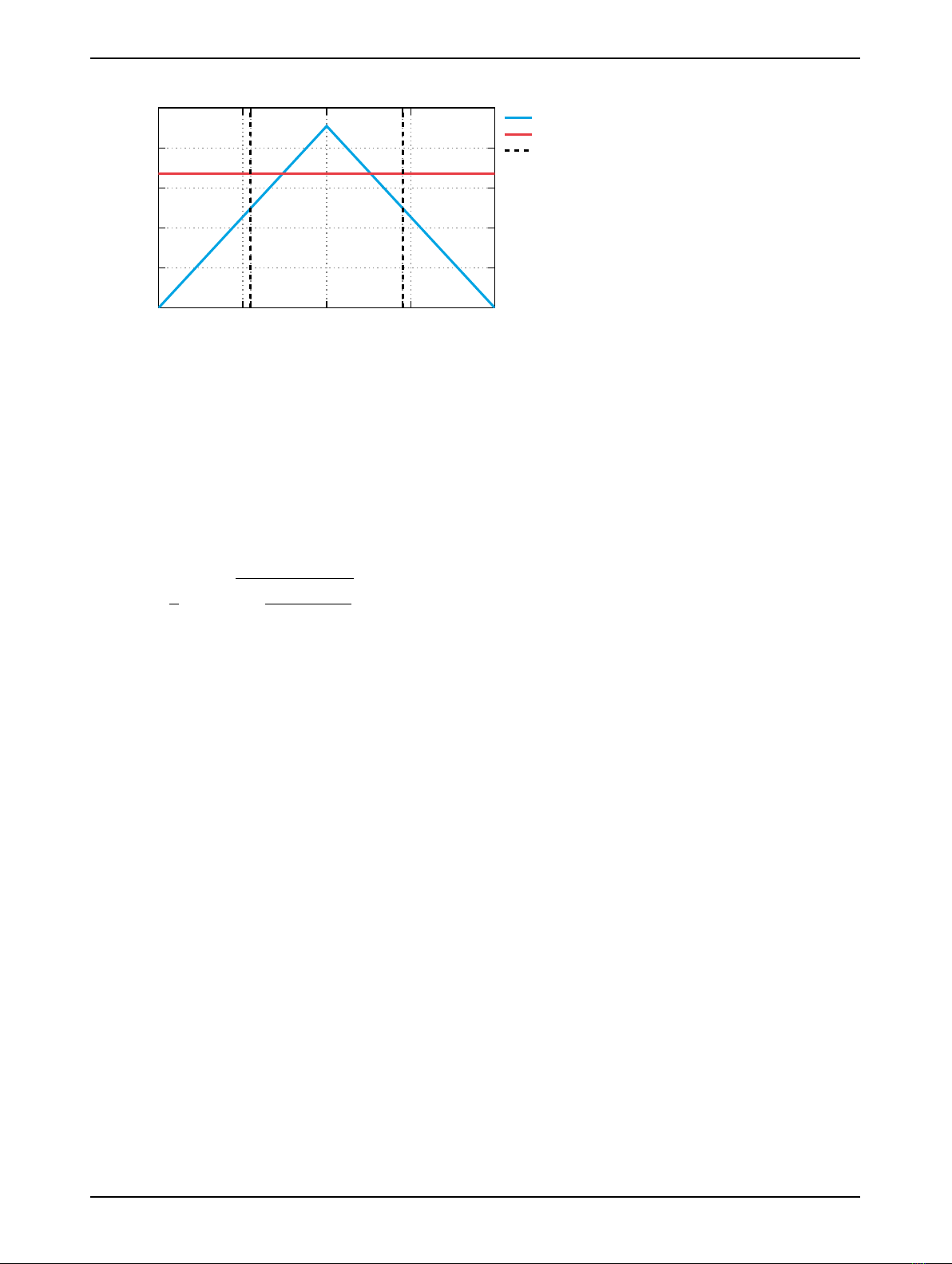
simple Triangular Wave Generator is used with Minimum signal value 0, Maximum signal value 1,
Frequency fsw,duty cycle 0, and Phase delay 0. This generates a ramp, which is 1 at the switching
instant and reaches 0 at the next switching instant.
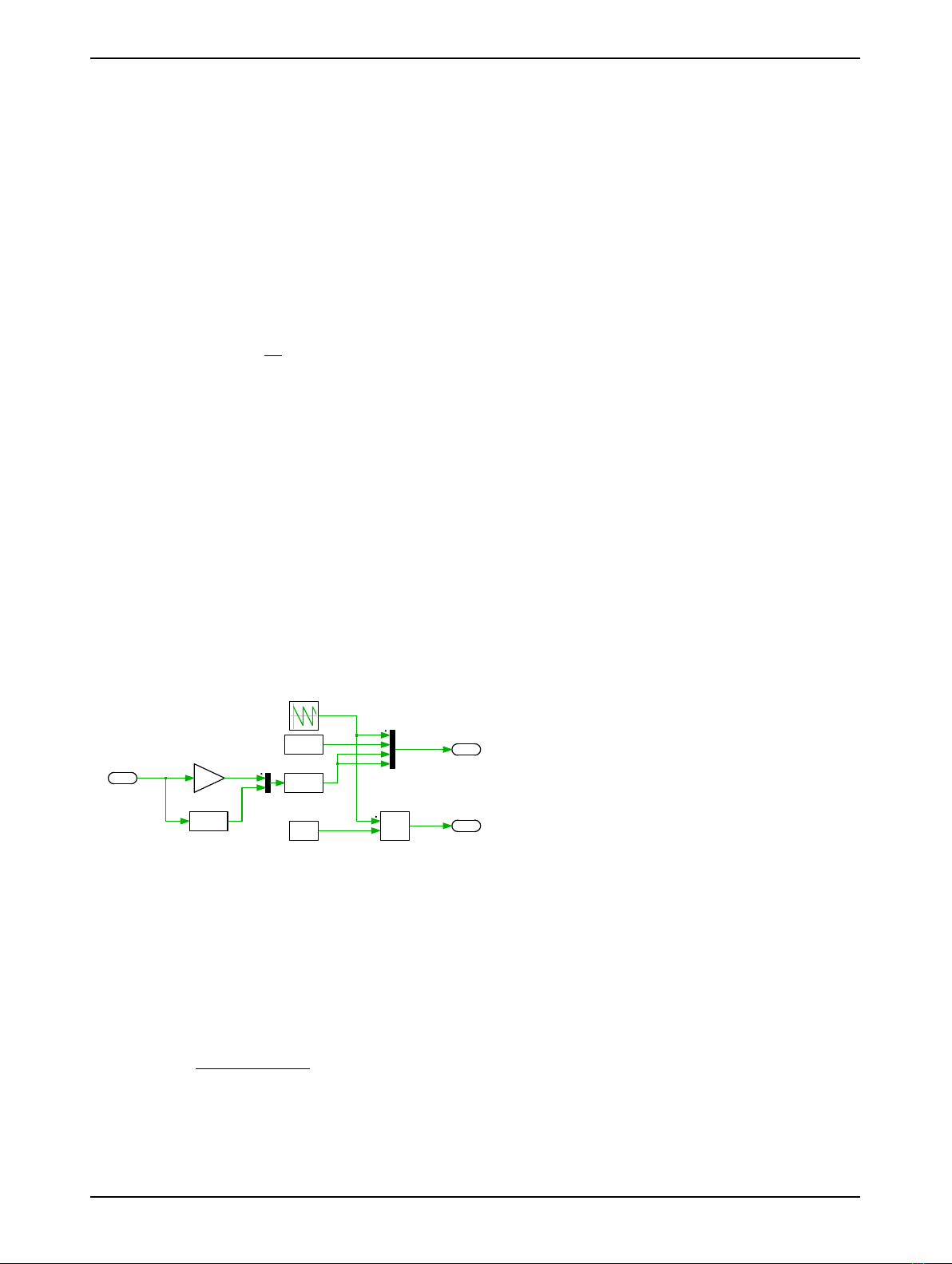
Fig. 8 shows the “phase shift generator” implementation.
PhaseShiftAngles
4PWMinp.u.
SamplingLevel
0.5=Midcycle
Figure 8: Schematic of the phase shift generator subsystem
Plant Linearization
As shown in Fig. 5, the Φ−ILV expression has been linearized for the controller design. The small
signal expression, derived from Eq. (1), between the perturbation of current (∆ILV) and phase shift
angle (∆Φ) is given by:
∆ILV(t) = VHV
2·π2·L·fsw ·n·(π−2·Φ) ·∆Φ(t) = KDABI·∆Φ(t)∀0≤Φ≤π. (4)
Fig. 9 shows the KDABIvalues for different operating points, where KDABIis the current gain as a lin-
ear function of phase angle. For the PI regulator tuning purposes it has been found that the use of a
linear approximation of KDABIis sufficiently accurate to model the closed-loop dynamics of the system
with relatively low closed-loop control bandwidths [2].
www.plexim.com 7