Atmel 80C51 Installation and operating instructions
Other Atmel Microcontroller manuals

Atmel
Atmel ATtiny104 Xplained Nano User manual

Atmel
Atmel ATmega328PB Xplained Mini Installation and operating instructions

Atmel
Atmel ATmega168PB Xplained Mini User manual

Atmel
Atmel 8051 User manual

Atmel
Atmel AVR ATtiny15L User manual

Atmel
Atmel AT91 Series User manual

Atmel
Atmel AVR365 User manual

Atmel
Atmel AT89STK-03 Installation manual

Atmel
Atmel AT90PWM2 User manual

Atmel
Atmel AVR ATtiny22 Instruction Manual

Atmel
Atmel AT43DK325 User manual

Atmel
Atmel AT89RFD-10/EVLB002 User manual

Atmel
Atmel AT18F-DK3 User manual

Atmel
Atmel AVR042 Installation and operating instructions

Atmel
Atmel ATmega32M1 User manual

Atmel
Atmel AT90USB162 User manual

Atmel
Atmel AT90S4433-8AC User manual
Atmel
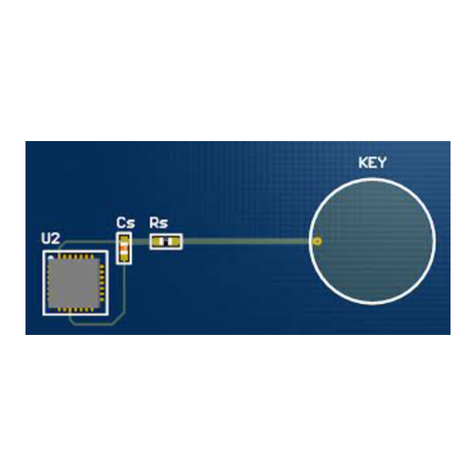
Atmel QTouch Installation and operating instructions

Atmel
Atmel ATF15 DK2 Series User manual

Atmel
Atmel AVR32 STK1000 User manual
Popular Microcontroller manuals by other brands

DIGITAL-LOGIC
DIGITAL-LOGIC MICROSPACE manual

Texas Instruments
Texas Instruments TMS320F2837 D Series Workshop Guide and Lab Manual

CYPRES
CYPRES CY14NVSRAMKIT-001 user guide

Espressif Systems
Espressif Systems ESP8266EX Programming guide

Abov
Abov AC33M8128L user manual
Silicon Laboratories
Silicon Laboratories C8051F800 user guide

























