Betzold Theodolit 86576 User manual

© Arnulf Betzold GmbH
Theodolit Nr./Art. 86576
Anleitung zu Nr./Art. 86421 / User Instructions for Nr./Art. 86421 /
Instruction pour Nr./Art. 86421 / Instructies voor Nr./Art. 86421

Deutsch
3
1. Allgemeine Hinweise zum Theodoliten
Bewahren Sie diese Hinweise zum späteren Gebrauch auf!
1.1. Anwendungsbereich und bestimmungsgemäße Verwendung
Der Theodolit ist ausschließlich für den Einsatz im Unterricht bestimmt.
Kinder sollen den Theodoliten nur unter der Aufsicht von Erwachsenen verwenden.
1.2. Warnhinweise
Achtung! Setzen oder lehnen Sie sich nicht auf den Theodoliten. Legen Sie keine schweren Gegenstände darauf ab.
Die Stativbeine können brechen. Es besteht Verletzungsgefahr! Nicht in der Nähe von Wärmequellen oder in der Sonne
lagern. Verpackungsfolie wegen Erstickungsgefahr sofort entsorgen.
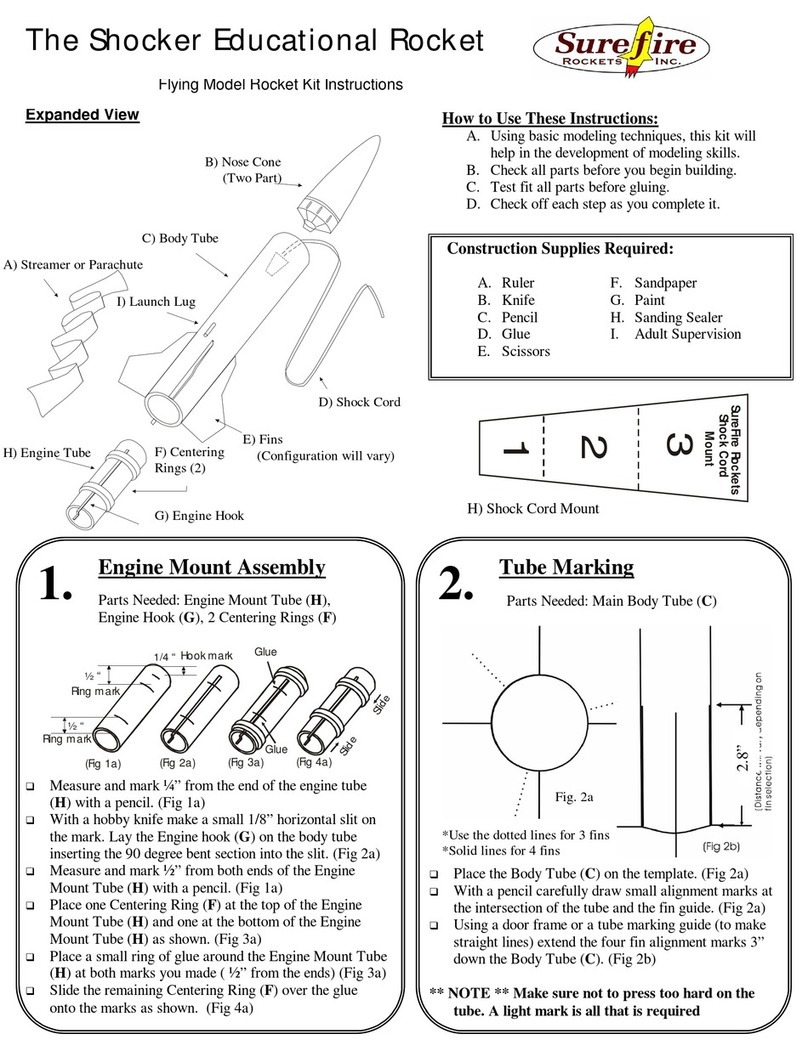
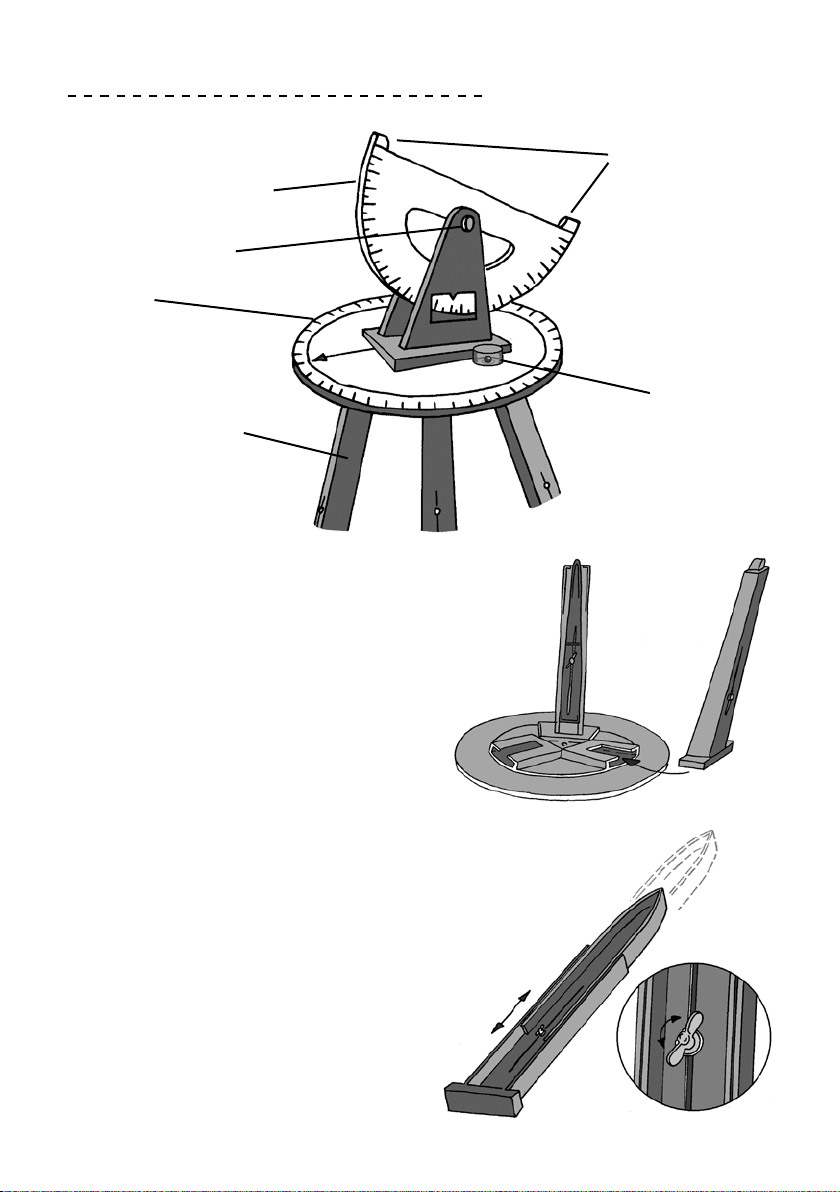
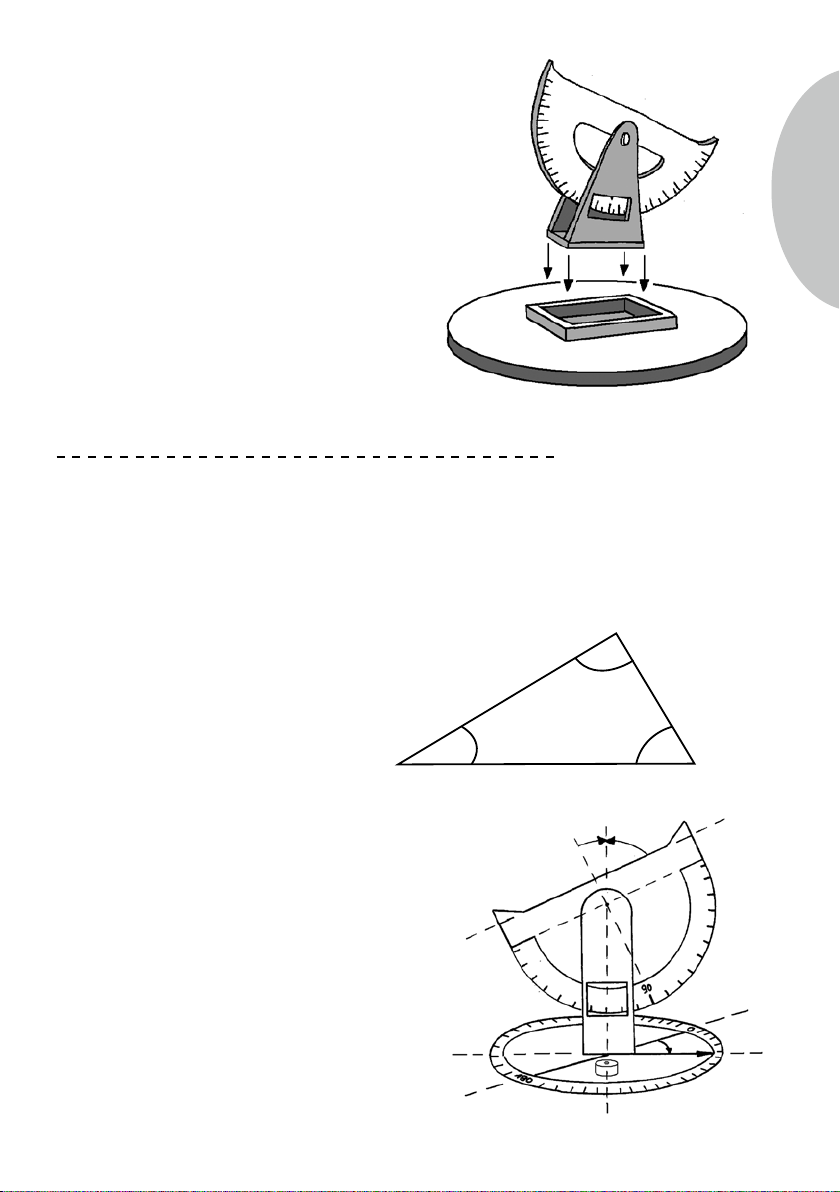
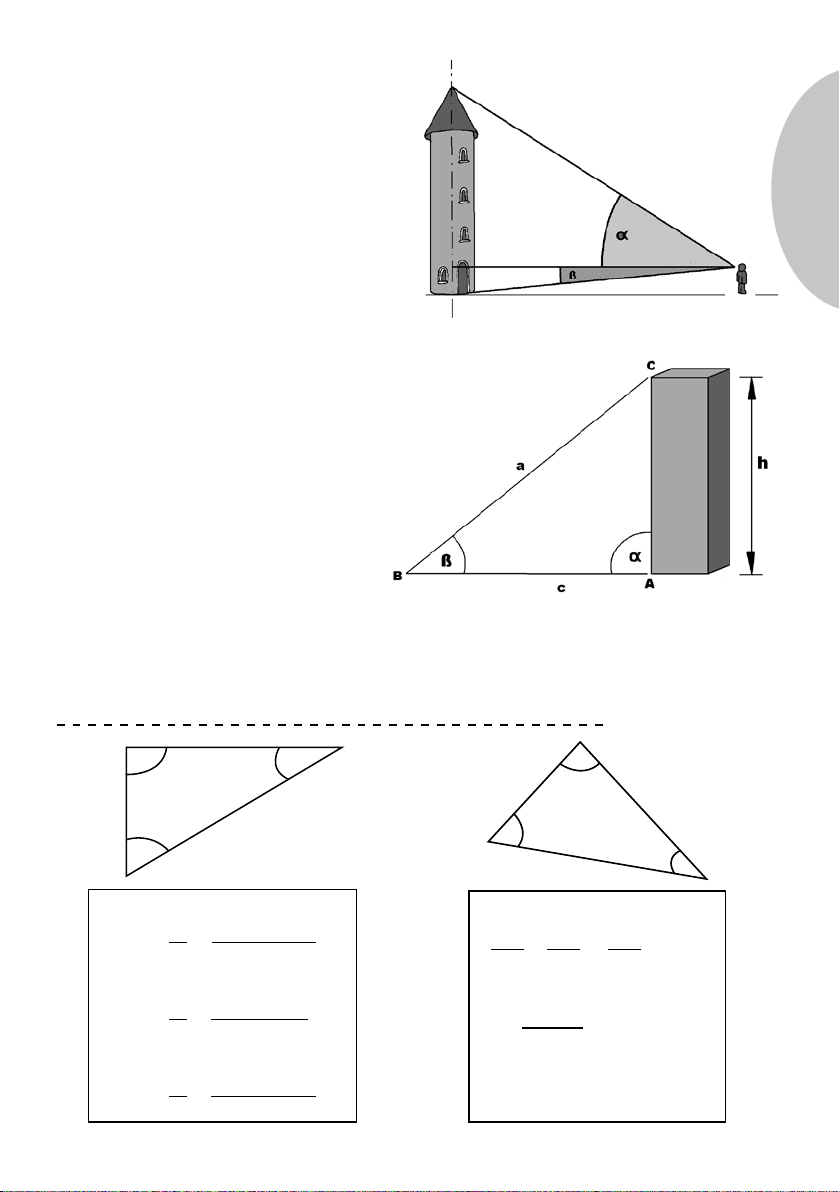
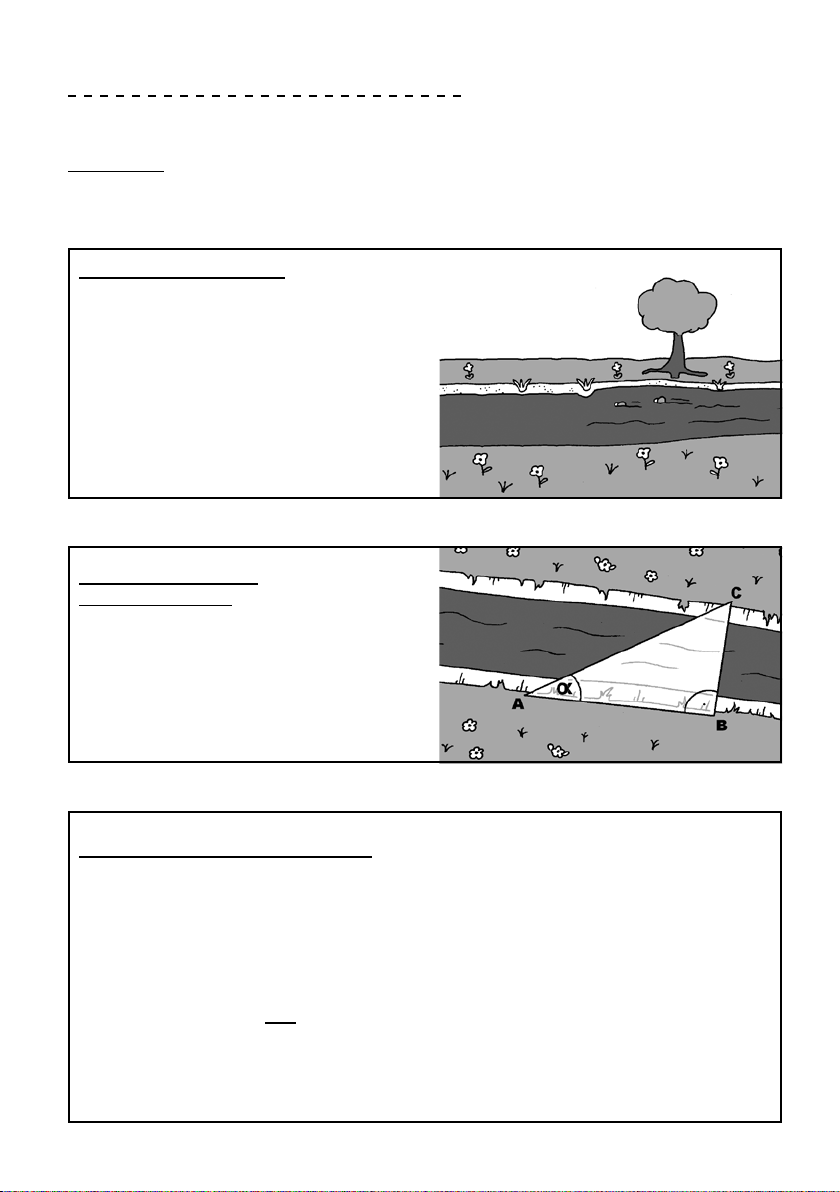
1.3. Was kann ich mit dem Theodoliten messen?
Der Theodolit ist ein Instrument zum Messen von Winkeln. Er wird in der Vermessungskunde zur Messung von Horizontal-
und Vertikalwinkeln eingesetzt.
1.4. Abmessungen und Gewicht
Der Theodolit lässt sich bis auf eine Höhe von 85 cm bis 127 cm einstellen. Er wiegt 1,9 kg.
1.5. Anwendungsbedingungen und Grenzen für Betrieb und Lagerung
• Nicht in der Nähe von Wärmequellen oder in der Sonne lagern.
Nur in trockenen Räumen lagern.
• Setzen oder lehnen Sie sich nicht auf den Theodoliten. Legen Sie keine schweren
Gegenstände darauf ab.
Die Stativbeine können brechen.
• Überprüfen Sie vor dem Betrieb, ob alle Schrauben, insbesondere die der Stativbeine,
fest angezogen sind.
1.6. Hinweise zur Entsorgung
Bitte entsorgen Sie die Verpackungsmaterialien nach dem Auspacken sofort.
Folien stellen eine Erstickungsgefahr für Kleinkinder dar.
1.7. Sicherer und korrekter Gebrauch
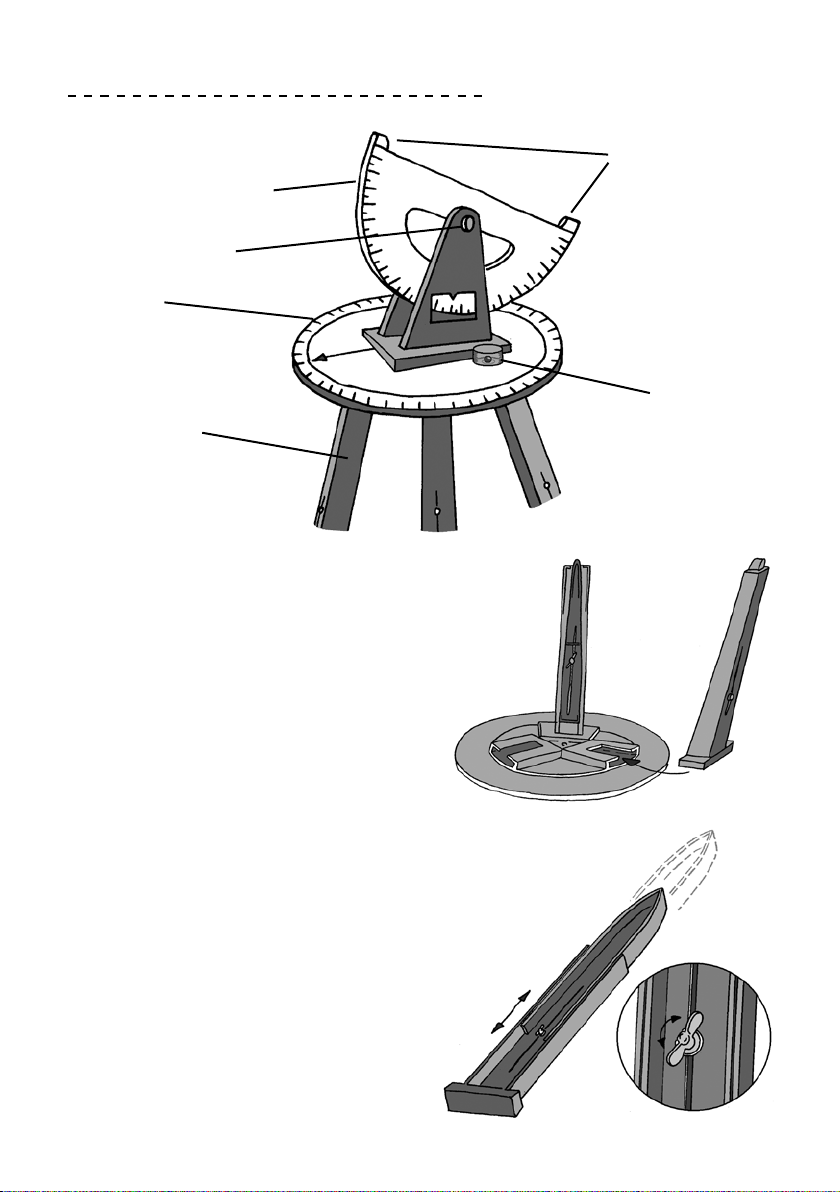
Überprüfen Sie vor dem Betrieb, ob alle Schrauben, insbesondere die der Stativbeine, fest angezogen sind. Kontrollieren
Sie ebenfalls, ob die Stativbeine bis zum Anschlag eingeschoben sind. Nur dann steht der Theodolit sicher. Prüfen sie, ob
die Alhidade fest auf den Horizontalkreis aufgesteckt ist.
1.8. Instandhalten und Reinigen durch den Benutzer
Wischen Sie die Bauteile ausschließlich mit einem feuchten Tuch ab. Verwenden Sie keine Reinigungsmittel. Lassen Sie
die Bauteile vor dem nächsten Gebrauch vollständig trocknen.
1.9. Ersatzteile und Reparatur
Anfragen zu Ersatzteilen und Reparatur richten Sie bitte an folgende Adresse:
siehe unter 1.10. Garantie
1.10. Garantie
Für die von uns gelieferte Ware gilt die gesetzliche Gewährleistungsfrist von 2 Jahren.
Die Frist beginnt mit der Ablieferung der Ware. Im Garantiefall wenden Sie sich bitte an Ihren Händler oder folgende
Adressen:
D
Arnulf Betzold GmbH
Ferdinand-Porsche-Str. 6
73479 Ellwangen
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.de
AT
Arnulf Betzold GmbH
Seebühel 1
6233 Kramsach/Tirol
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.at
CH
Betzold Lernmedien GmbH
Winkelriedstrasse 82
8203 Schaffhausen
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.ch

4
2. Wie baue ich den Theodoliten auf?
a) Bauteile des Theodoliten
1. Schieben Sie die 3 Stativbeine auf der
Unterseite des Horizontalkreises ein.
Schieben sie diese bis zum Anschlag nach
hinten. Die Flügelschrauben müssen nach
innen zeigen.
Alhidade (mit Vertikalkreis)
Kippachse
Stativteller
(mit Horizontalkreis
mit Messskala)
verstellbares Dreibein-
Stativ
Dosenlibelle
Visierung (mit Kimme und
Korn)
2. Die Stativbeine sind mittels Flügelschrauben
einzeln höhenverstellbar. Drehen Sie dazu
die Flügelschraube an der Innenseite der
Stativbeine auf, verstellen Sie das Stativbein
auf die gewünschte Höhe und drehen Sie
die Flügelschraube wieder zu.

Deutsch
5
3. Anwendung des Theodoliten im Unterricht
Der Theodolit ist ein Instrument zum Messen von Winkeln. Es wird in der Vermessungskunde zur Messung von Horizontal-
und Vertikalwinkeln eingesetzt.
Mit dem Theodoliten werden Winkel gemessen. Diese sind die Grundlage für weitere Vermessungen und immer größer
werdende Dreiecksnetze.
Durch Winkelmessung in den Eckpunkten des Dreiecks und die Messung der Grundlinie entsteht ein Dreieck, in dem eine
Seite und die drei Winkel bekannt sind. Daraus kann man dann die weiteren Seitenlängen errechnen.
Die Winkel werden am Horizontal- bzw.
Vertikalkreis abgelesen.
3. Stecken Sie die Alhidade auf die vorgege-
bene Stelle auf dem Horizontalkreis.
4. Stecken Sie die beiden Fernrohrträger fest
auf die Alhidade. Die Steckplätze erkennen
Sie an den Aussparungen.
5. Auf die Fernrohrträger können Sie ein
Hand-Fernrohr mit einem Durchmesser bis
zu ca. 4 cm aufstecken.
(Das Fernrohr ist nicht im Lieferumfang
enthalten.)
Der Theodolit hat 4 Achsen:
a) Stehachse S:
die vertikale Drehachse des Theodoliten
b) Kippachse K:
die horizontale Achse, um die sich das Diopter
neigt
c) Zielachse Z:
die Achse, die durch das Diopter mit Kimme
und Korn läuft.
d) Libellenachse L:
Achse durch Libellenmittelpunkt und Kippachse
KZ
L
S

6
c) Messung von Vertikalwinkeln
Ein Höhenwinkel α ist der Winkel eines Punktes über einer Referenzäche (z. B. dem Horizont).
Ein Tiefenwinkel β ist der Winkel eines Punktes unter einer Referenzäche (z. B. dem Horizont).

Deutsch
7
Höhenwinkel αmessen:
Stellen Sie den Vertikalkreis auf 0.
Messen Sie nun den Höhenwinkel, indem Sie
den Punkt C anvisieren.
Lesen Sie den Winkel auf dem Vertikalkreis ab.
Tiefenwinkel βmessen:
Stellen Sie den Vertikalkreis auf 0.
Messen Sie nun den Tiefenwinkel, indem Sie
den Punkt A anvisieren.
Lesen Sie den Winkel auf dem Vertikalkreis ab.
d) Messung von Höhen
Die Messung von Höhen erfolgt über zwei Winkel und eine Strecke.
Messen Sie die Strecke c (von B nach A).
Winkel α ist ein rechter Winkel mit 90°.
Winkel β messen Sie mit dem Theodoliten.
Mit folgender Winkelfunktion errechnen Sie
die Höhe h:
tan β = h : c
Bsp. c = 50 m; β = 26°
tan 26° = h : 50 | • 50
h = tan 26° • 50
h = 24,5
3.3. Einige Formeln zur Berechnungen im Dreieck
c2 = a2+ b2
sin α= =
cos α = =
tan α = =
a Gegenkathete
c Hypothenuse
b Ankathete
c Hypothenuse
a Gegenkathete
b Ankathete
Sinussatz:
a b c
sin αsin βsin γ
Beispiel:
b • sin α
sin β
Cosinussatz:
c2 = a2+ b2- 2 • a • b • cos γ
=
a =
=
C
A
β
α
a
b
c
β
a
α
b
c
γ

8
3.4. Aufgaben mit dem Theodoliten
Wir messen die Breite eines Flusses
Vorbereitung:
Ist kein geeigneter Fluss in der Nähe vorhanden, markieren Sie den Fluss einfach mit Kreide auf dem
Schulhof.
Aufgabe: Flussbreite messen
Gruppe von 3 - 4 Schülern
Material: 1 Theodolit
1 Maßband
3 Pöcke oder Markierungskegel
1 Seil
Aufgabe: Wie kann man die Breite eines Flusses
messen?
Dokumentiert euer Verfahren mit Skizzen und einer
Beschreibung.
Lösungshilfe zu Aufgabe
„Flussbreite messen“
Um die Breite eines Flusses zu messen, ist eine
Strecke |AB| = 10 m abgesteckt worden.
Wie breit ist der Fluss?
Lösung zu Aufgabe „Flussbreite messen“
Breite des Flusses = 62,5 m
|AB| = 10 m
β = 90°
Bestimme mit Hilfe des Theodoliten den Winkel α.
Nun ergibt sich aus tan α = die Lösung.
tan α = |BC| : 10 | • 10
|BC| = tan α • 10
|BC|
|AB|

English
9
1. General information about the theodolite
Please keep these instructions in a safe place for future consultation!
1.1. Area of application and correct use
The theodolite is intended exclusively for use during lessons.
Children should only use the theodolite under adult supervision.
1.2. Warnings
Warning! Do not sit or lean on the theodolite. Do not place any heavy items on it. The tripod legs could break. Possible
danger of injury. Do not store near heat sources or in direct sunlight. Immediately dispose of the packaging lm to prevent
any risk of suffocation.
1.3. What can I measure with the theodolite?
The theodolite is an instrument for measuring angles. It is used in surveying to measure
horizontal and vertical angles.
1.4. Dimensions and weight
The theodolite can be adjusted to a height of between 85 cm and 127 cm.
It weighs 1,9 kg.
1.5. Conditions of use and operation and storage instructions
• Do not store close to heat sources or in direct sunlight. Store in a dry place.
• Do not sit or lean on the theodolite. Do not place any heavy items on it.
The tripod legs could break.
• Screws, especially those on the tripod legs, are tightly fastened.
1.6. Advice on disposal
Please dispose of the packaging materials immediately after unpacking.
The lms carry a risk of suffocation for small children.
1.7. Safe and correct use
Before usage check that all screws, especially those of the tripod legs, are tightly fastened.
Also make sure that the tripod legs are pushed in as far as they will go.
This is essential for the stability of the theodolite.
Make sure that the alidade is rmly mounted on the horizontal circle.
1.8. Maintenance and cleaning by the user
Wipe the parts only with a damp cloth. Do not use any cleaning product.
Allow the parts to dry completely before the next use.
1.9. Spare parts and repair
Please send any queries about spare parts and repairs to the following address:
see under 1.10. Guarantee
1.10. Guarantee
The products supplied by us are covered by a 2-year guarantee.
The guarantee period begins with the delivery of the product.
To exercise the guarantee, please contact your dealer or the following addresses:
D
Arnulf Betzold GmbH
Ferdinand-Porsche-Str. 6
73479 Ellwangen
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.de
AT
Arnulf Betzold GmbH
Seebühel 1
6233 Kramsach/Tirol
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.at
CH
Betzold Lernmedien GmbH
Winkelriedstrasse 82
8203 Schaffhausen
Telefon: [phone]
Telefax: [phone]
E-Mail: [email protected]
www.betzold.ch

10
2. How do I assemble the theodolite?
a) Theodolite parts
1. Insert the 3 tripod legs into the slots on the
bottom side of the horizontal circle. Push
them back as far as they will go. The thumb
screws should point inwards.
alidade (with vertical circle)
tilting axis
tripod head
(with horizontal circle
with measuring scale)
adjustable tripod
circular spirit level
sight (with eye piece and
objective)
2. The tripod legs can be individually adjusted
using thumb screws.
To do so, unscrew the thumb screw on the
inside of the tripod legs, adjust the tripod
legs to the desired height then retighten
the thumb screw.